GRASS GIS pas à pas pour les débutants: 7 - les modules d'interpolation spatiale: introduction, passage d'une couche vectorielle à une couche matricielle (v.to.rast) et d'une couche vectorielle 2D à une d'une couche vectorielle 3D (v.to.3D, v.drape)

	Niveau	Débutant
	Logiciels utilisés	GRASS GIS
	Plateforme	Windows | Mac | Linux | FreeBSD

 

Une des particularités de GRASS GIS les plus demandées sur les forums est l'interpolation des surfaces, comme un MNT, par exemple. C'est normal puisqu'avec la plupart des « grands » logiciels SIG, il faut payer pour avoir des extensions qui se basent pourtant sur les mêmes principes que ceux de GRASS GIS. De surcroît, dans le monde francophone, rares sont les institutions qui donnent des cours sur GRASS...

En effet, dès le début de l'histoire de celui qui est devenu le doyen des logiciels SIG, cet aspect a été pris en considération.

Nous ne pouvons passer sous silence le rôle de Helena Mitasova (www.meas.ncsu.edu/faculty/mitasova/mitasova.html), professeur à la North Carolina State University (NCSU) dans le Marine, Earth, & Atmospherical Science (MEAS), skagit.meas.ncsu.edu/~helena/, qui a analysé théoriquement les principaux algorithmes et les a implémentés dans GRASS et ce, depuis la fin des années 1980. Elle a développé, entre autres choses, les principes des méthodes d'interpolation par splines (en.wikipedia.org/wiki/Spline_interpolation) dans les SIG (skagit.meas.ncsu.edu/~helena/gmslab/papers/MG-I-93.pdf, entre autres articles) et son implémentation dans GRASS GIS.

Ces méthodes ont été reprises bien après par les autres logiciels dans des extensions comme Spatial Analyst et 3D Analyst pour ArcGIS, avec ses travaux comme référence.

Elle est aussi la coauteure du livre www.grassbook.org/, avec Markus Neteler.

Elle a reçu le prix Sol Katz Award de l'OSGEO en 2010 (www.osgeo.org/node/1069). Ces divers cours sont régulièrement cités et ses figures utilisées dans beaucoup de travaux (skagit.meas.ncsu.edu/~helena/gmslab/viz/sinter.html, ou skagit.meas.ncsu.edu/~helena/gmslab/papers/sint.html, par exemple).

Je suppose aussi que si vous lisez cet article, vous connaissez les principes et les méthodes de l'interpolation spatiale et je ne reviendrai pas en détail sur le sujet (il existe de meilleurs tutoriels que ceux que pourrais faire, notamment ceux d'ESRI) pour me focaliser sur leur application dans GRASS GIS.

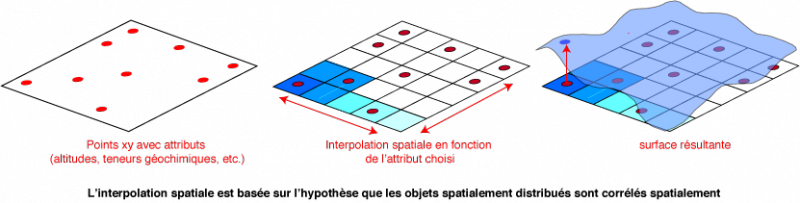
Signalons que c'est avec GRASS GIS que les premiers MNT pour l'étude géologique de la planète Mars ont été réalisés (www.isprs.org/proceedings/XXXV/congress/comm4/papers/455.pdf)

Le thème sera abordé de la manière suivante, en plusieurs parties:

Considérations préalables

Il existe de nombreux algorithmes d'interpolation spatiale, mais il ne faut cependant pas se leurrer, aucune méthode n'est « meilleure » que les autres, car tout va dépendre de ce que l'on attend du résultat, même celles qui sont à la mode dans les questions sur les forums, les TINs et celles résultant du Krigeage géostatistique.

• Certaines méthodes sont basées sur un partitionnement de l'espace, d'autres sur la création de grilles:

figure modifiée à partir de www.arch.mcgill.ca/prof/klopp/arch678/fall2008/3%20Student%20exchange/Team%204/tk%20studio/Oct21/voronoi.ai

• Certaines méthodes forcent les surfaces à passer par tous les points, d'autres mettent l'accent sur le lissage de la surface et certaines sont plus complexes que d'autres.

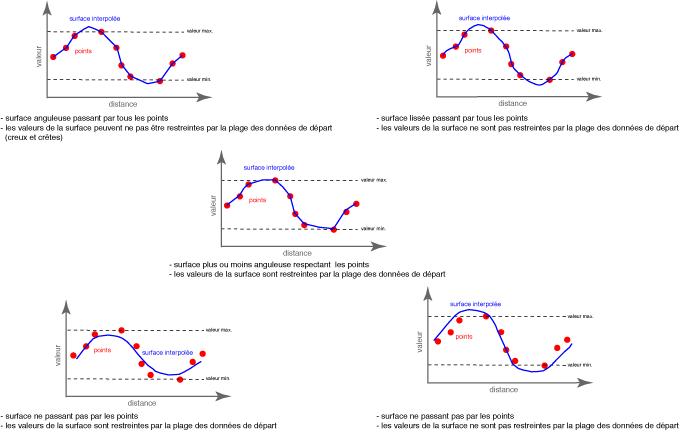
• Il existe, dans GRASS aussi, des techniques plus ou moins complexes pour
  • comparer ces surfaces entre elles;
  • calculer les indicateurs d'écart entre les valeurs observées et les valeurs calculées; (MSE, erreur quadratique moyenne, moyenne des carrés des résidus ou erreur-type RMSE (root-mean-square error), etc.;
  • mais aucune ne fournira un résultat univoque, ne permettra de dire quelle est la « meilleure ».
• C’est, de plus, l'un des grands domaines d'application du calcul de propagation des incertitudes qui a été abordé dans Logiciels SIG, erreurs, incertitudes, propagation des incertitudes ou les grands oubliés dans les traitements courants... 

Historique

Historiquement, GRASS GIS étant un SIG à vocation raster, des solutions comme la technique d'interpolation par splines régularisées avec tension (implémentée par Helena Mitasova et son équipe) ont été privilégiées alors que les autres logiciels SIG en étaient encore aux TINs, technique datant des années 1970...

• On pouvait dire alors « et non, pas de TINs sur GRASS », mais cela a changé avec la refonte du module v.delaunay par Martin Pavlovsky en 2008 (résultat d'un « Google Summer of Code ») qui permet maintenant de créer une triangulation de Delaunay en 3D en gérant les triangles comme des « faces » (polygones 3D, voir GRASS GIS : géométries, topologies et conséquences pratiques (vecteurs, rasters, volumes))

De même, le Krigeage géostatistique, pouvait toujours être utilisé, mais en combinaison avec le progiciel R et en ligne de commandes seulement (voir Grass Gis, ses amis Python et R, ou la puissance d'un shell pas si "ringard" que ça... (traitement des données, géostatistiques and Co.)).

• l'adoption de Python a permis l'apparition de modules autonomes comme v.krige.py qui permettent de tout faire de manière transparente avec une interface (mais R est toujours nécessaire).

Les modules

Pour des raisons historiques, ceux-ci sont disséminés entre les menus Vecteurs et Raster:

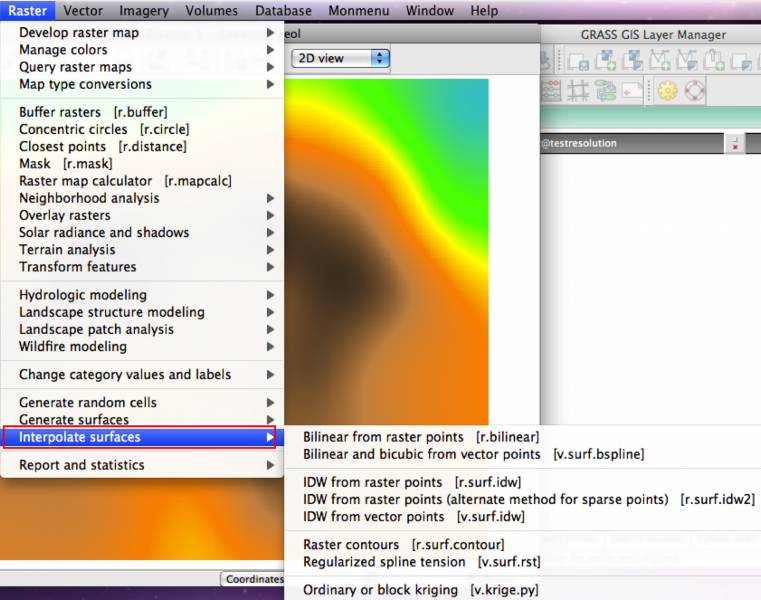
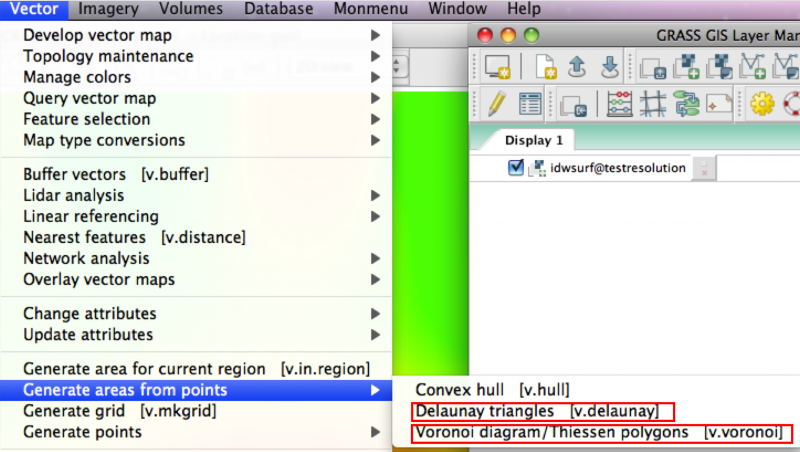
Ceux-ci sont:

1. dans le menu Vecteurs
   1. v.delaunay -> interpolation de Delaunay à partir de couches vectorielles.
   2. v.voronoï -> polygones de Voronoï à partir de couches vectorielles.
2. dans le menu Rasters
   1. r.bilinear -> interpolation bilinéaire à partir de couches matricielles (raster, module dépassé qui ne sera pas abordé dans la suite)
   2. v.surf.idw -> interpolation par pondération inverse de la distance (IDW, Inverse Distance Squared Weighting.) à partir de couches vectorielles.
   3. r.surf.idw et r.surf.idw2 -> interpolation par pondération inverse de la distance (IDW, Inverse Distance Squared Weighting.) à partir de couches matricielles (résultats en virgule flottante pour le deuxième)
   4. v.surf.rst -> interpolation par splines régularisées avec tension (RST, regularized splines with tension) à partir de couches vectorielles.
   5. v.surf.bspline -> interpolation par splines bilinéaires ou bicubiques avec régularisation de Tykhonov à partir de couches vectorielles
   6. v.krige.py -> interpolation par Krigeage ordinaire à partir de couches vectorielles.
   7. r.surf.contour -> interpolation à partir de couches isolignes (contours) matricielles (raster).

Il y a aussi moyen de construire des surfaces « théoriques », sans interpolation de valeurs. Ce sont les modules (ils ne seront pas vus dans la suite):

1. Dans le menu Raster/Generate surface
   1. r.surf.fractal -> création d'une surface en fonction d'une dimension fractale
   2. r.surf.gauss -> création d'une surface basée sur un générateur gaussien de nombres
   3. r.plane -> création d'une surface plane à partir d'un point, d'une pente ou pendage pour les géologues, et d'une direction  (azimut)
   4. r.random.surface -> création d'une surface aléatoire
   5. r.surf.random -> création d'une surface aléatoire dont la déviation peut être fixée par l'utilisateur
   6. v.kernel -> création d'une surface de densité à partir d'une couche vectorielle sur base de kernels mobiles

Modularité de GRASS GIS et modules complémentaires

La grande force de GRASS réside dans son extrême modularité. Il est toujours possible de créer et/ou d'ajouter des modules non standards complémentaires:

• en combinant des commandes comme expliqué dans GRASS GIS pour les experts: 1 - créer son propre module: r.in.rgb (importation directe d'un raster en couleur) en Python avec un menu pour le lancer, par exemple;
• en créant de nouveaux modules qui vont utiliser d'autres programmes installés comme R, par exemple.

Ces modules complémentaires se trouvent principalement sur grass.osgeo.org/wiki/GRASS_AddOns, mais il y a d'autres sites qui en proposent aussi surtout depuis l'adoption de Python.

Notons que ceux qui utilisent d'autres programmes ne sont généralement pas disponibles sur Windows qui n'a pas de compilateur par défaut comme Linux ou Mac OS X. Il faut aussi que l'application tierce soit disponible en ligne de commandes. Certains d'entre eux sont néanmoins disponibles à wingrass.fsv.cvut.cz/grass64/addons/grass-6.4.2/

Le module GRASS GEM est théoriquement destiné à installer automatiquement ces modules complémentaires, mais il n'est pas très efficace pour le moment... Pour Mac OS X, la solution alternative proposée par William Kyngesburye (www.kyngchaos.com/) a été présentée sur le ForumSIG : GRASS 6.x Mac OS X: comment installer un module supplémentaire ("add-on").

Quelques modules complémentaires utiles

• v.triangle d'Alexander Muriy -> qui permet de créer des TINs avec des lignes de fracture (breaklines, voir grass.osgeo.org/wiki/TIN_with_breaklines). En pratique, c'est une interface pour le programme Triangle de Jonathan Richard Shewchuk (www.cs.cmu.edu/~quake/triangle.html) qui doit donc être préalablement installé;
• v.trimesh de Jaime Carrera -> qui permet de créer des TINs à partir de couches vectorielles surfaciques (www.valledemexico.ambitiouslemon.com/vtrimesh.html ) qui se base aussi sur la librairie/programme Triangle;
• r.surf.nnbathy de Maciej Sieczka -> (www.sieczka.org/prog/grass/r.surf.nnbathy.html ) qui propose trois algorithmes de triangulation dont celui de Delaunay et deux du plus proche voisin. Il nécessite que la librairie nc avec le programme nnbathy (code.google.com/p/nn-c/) de Pavel Sakov et Triangle soient préalablement installés.

                        triangulation de Delaunay avec  v.delaunay -> couche vectorielle
                        triangulation de Delaunay avec r.surf.nnbathy et l'algorithme linéaire -> couche matricielle

À ma connaissance, ces modules ne sont pas disponibles sur Windows, mais fonctionnent très bien sur Mac OS X ou Linux après compilation et installation de nc et de Triangle.

• tin.to.raster.py de Antonio Alliegro ->  digilander.libero.it/antonioall/python_tin2raster.html (en italien) qui permet de transformer le résultat vectoriel de v.delaunay en surface matricielle 3D;
• v.autokrige de Mathieu Grelier -> qui permet de faire de l'interpolation par Krigeage de manière plus simple qu'avec v.krige (toujours en se basant sur R qui doit être installé et disponible en ligne de commandes).

Les puristes diront certainement « oui, mais il faut que ces programmes supplémentaires soient aussi installés, ce qui n'est pas le cas dans d'autres logiciels SIG où tout est disponible nativement ».  Et alors, pourquoi refaire deux fois la même chose, vive la collaboration et aux utilisateurs de GRASS, la puissance d'extensions comme gstat !

Les données de départ

Dans GRASS GIS, une surface matricielle peut être créée à partir:

• de points 2D ou 3D, sous forme de couches vectorielles ou de couches matricielles;
• d'isolignes comme les contours ou les courbes de niveau (lignes 2D ou 3D) sous forme de couches vectorielles ou de couches matricielle.

(Le module non standard v.trimesh permet de travailler à partir de couches vectorielles surfaciques).

Les données test pour la suite des traitements

La couche vectorielle est composée de 100 points 3D générés aléatoirement avec des altitudes qui s'étagent de 330 à 420 m et c'est bien cette variable altitude qui sera interpolée (puisque c'est le sujet le plus demandé sur les forums). Il est maintenant évident, après avoir lu les autres articles introductifs, qu'il faut fixer préalablement une région pour les traitements de couches matricielles. Elle est fixée ici sur l'emprise et la résolution de cette couche vectorielle de départ.

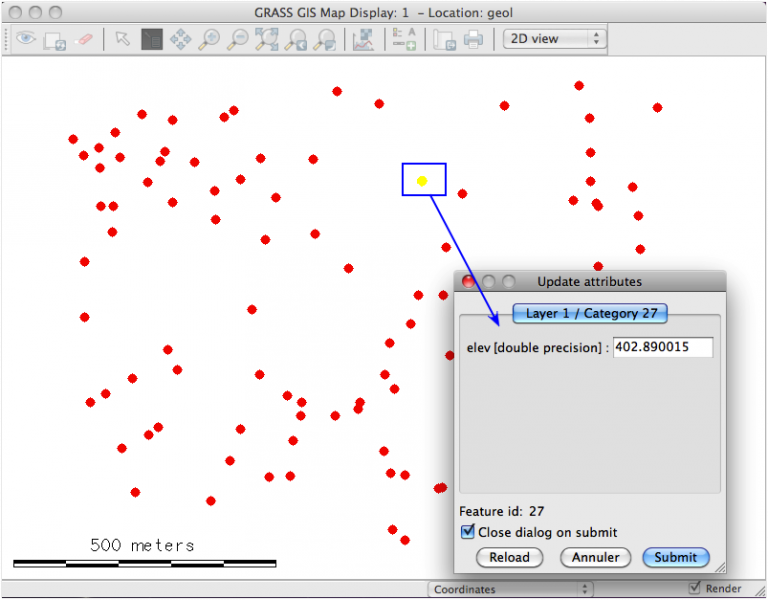
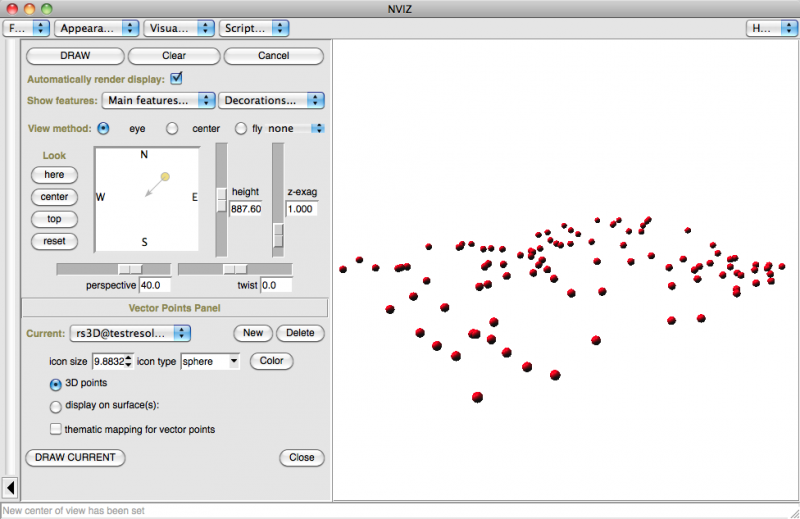
                                                                 dans nviz

Comme je suis géologue, lorsque la méthode est adéquate, je montrerai aussi comment créer une surface à partir des couches recoupées par des sondages (limite ensemble bleu - ensemble rouge):

 

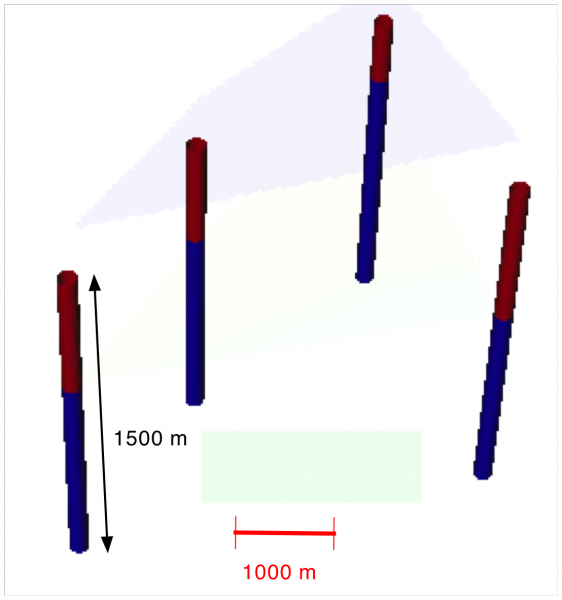
Avant de débuter, quelques transformations...

couches vectorielles en couches matricielles

Certains modules nécessitent que la couche en entrée soit au format matriciel (raster). Comment alors transformer une couche au format vectoriel avec des attributs qu'il est possible de traiter en couche matricielle, à priori dépourvue d'attributs ?

C'est là une des grandes forces de GRASS GIS puisqu'il dispose d'une telle fonctionnalité:

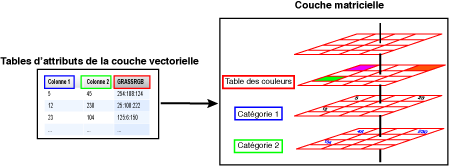
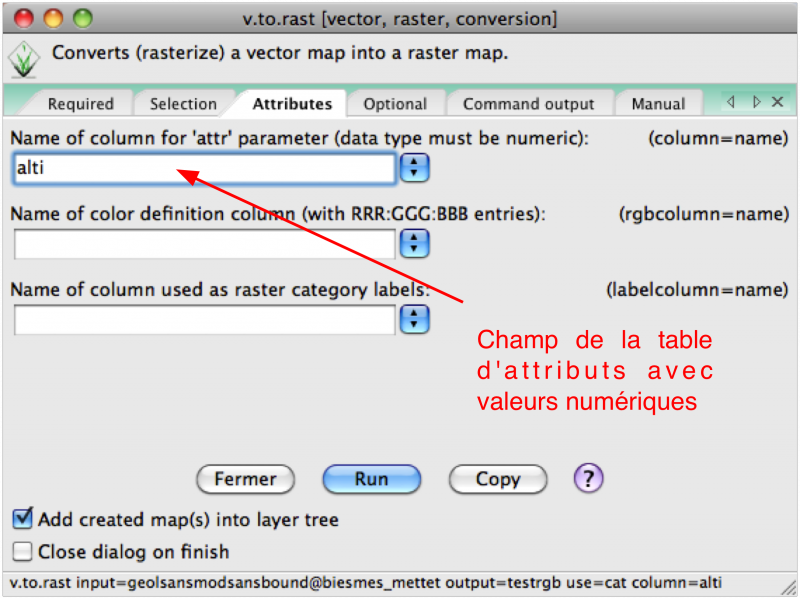
Cela se fait avec la commande v.to.rast (menu File/Map type Conversion):

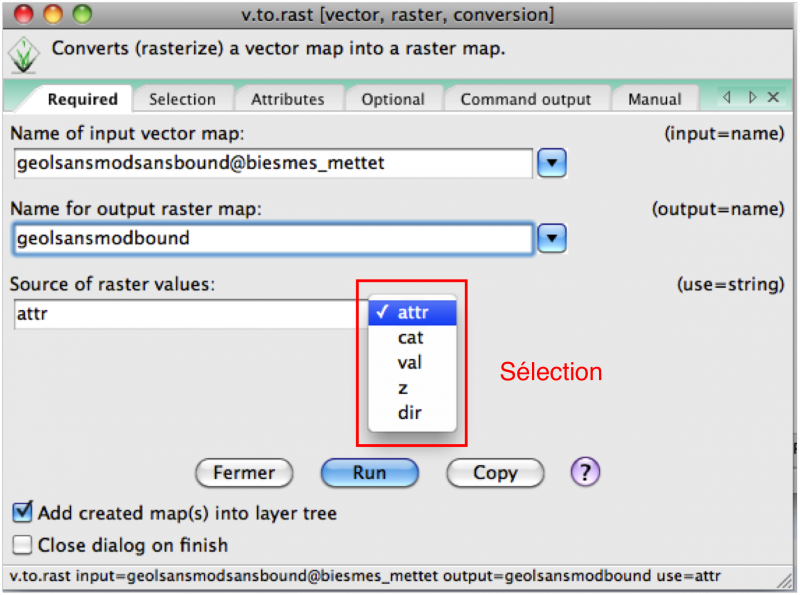
• attr - valeurs d'un champ de la table d'attributs (numérique)
• cat - catégories = valeurs d'un champ de la table d'attributs (non numérique)
• val - valeur spécifiée 
• z - coordonnées z d'un point ou d'une ligne de contour
• dir - sortie comme une direction de flux (en degrés, uniquement pour les lignes)

Application

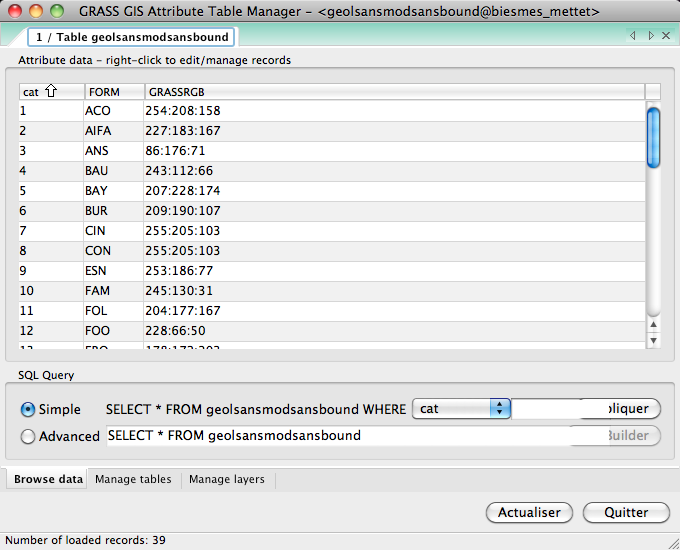
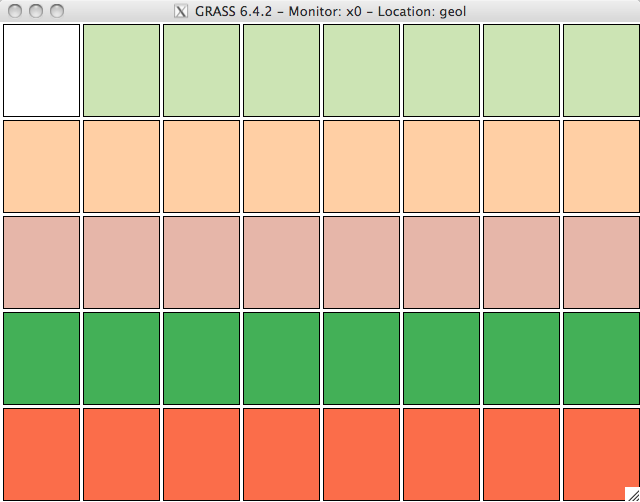
Soit la couche vectorielle suivante (carte géologique):

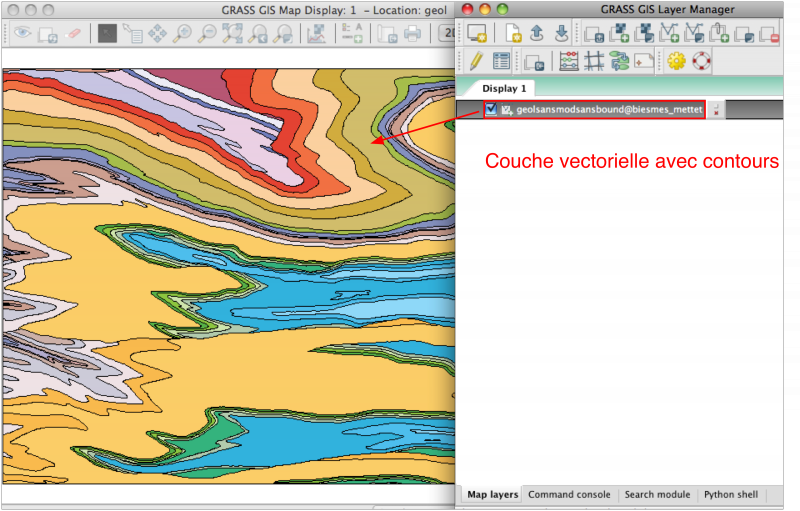
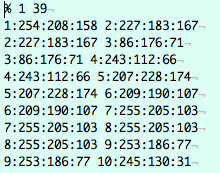
avec la table d'attributs (FORM = Formations géologiques, GRASSRGB = couleur):

Spécifions dans v.to.rast:

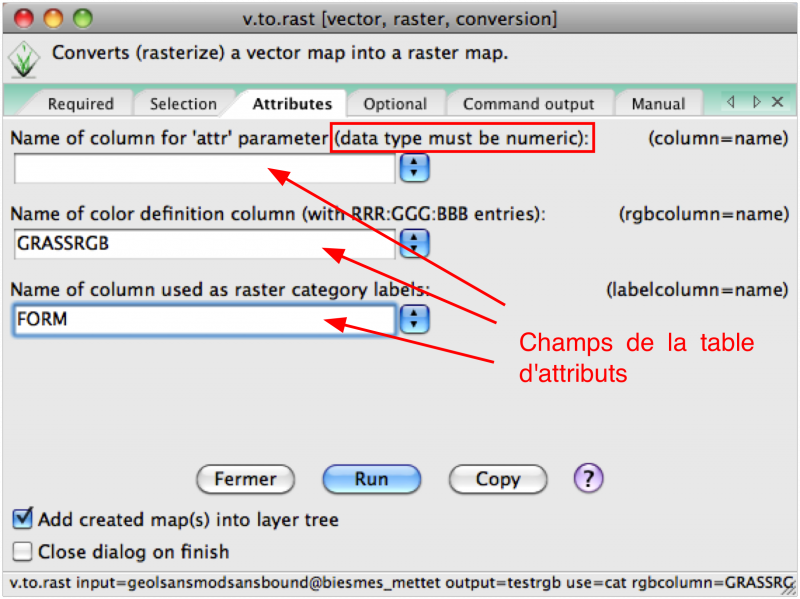
Je choisis ici l’option cat puisque mon champ n'est pas numérique (FORM).

Résultat

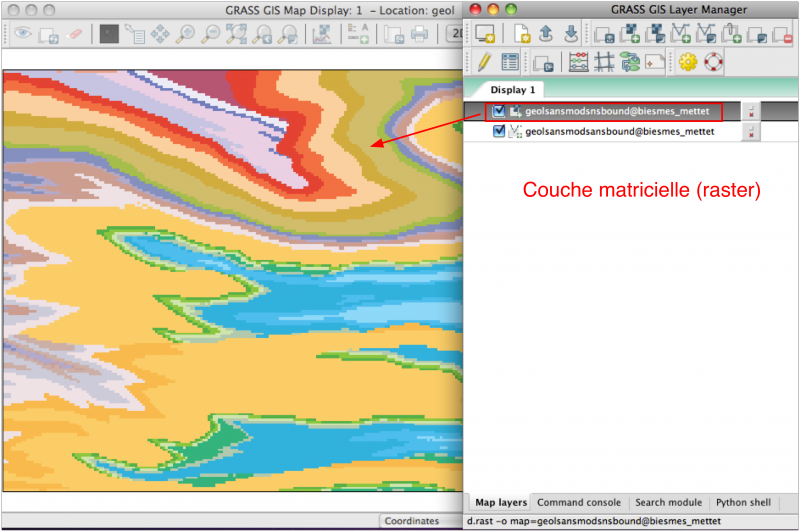
et les catégories résultantes sont bien conformes au champ FORM de la table attributaire:

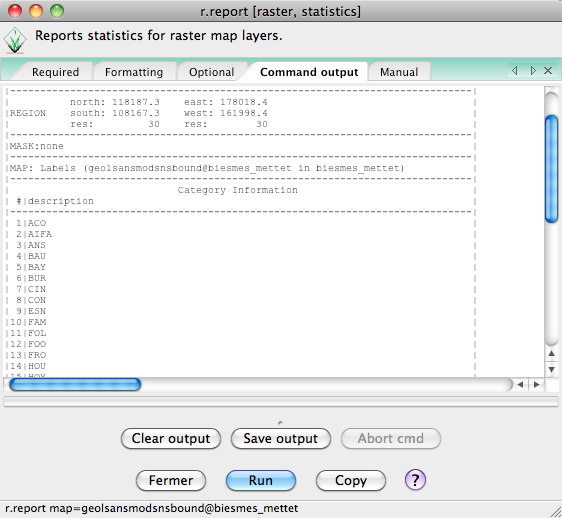
de même que la table des couleurs qui est construite à partir de l'attribut GRASSRGB:

Dans le cas qui nous concerne, avec l'altitude comme variable :

    couche vectorielle points vers couche raster points      

   couche vectorielle lignes vers couche raster lignes       

La commande sera donc:

couche vectorielle 2D en couche vectorielle 3D

Certains modules demandent que la couche en entrée soit une couche vectorielle 3D :

couche vectorielle points 2D vers couche vectorielle 3D

   couche vectorielle lignes 2D vers couche vectorielle 3D 

Cela se fait avec deux modules:

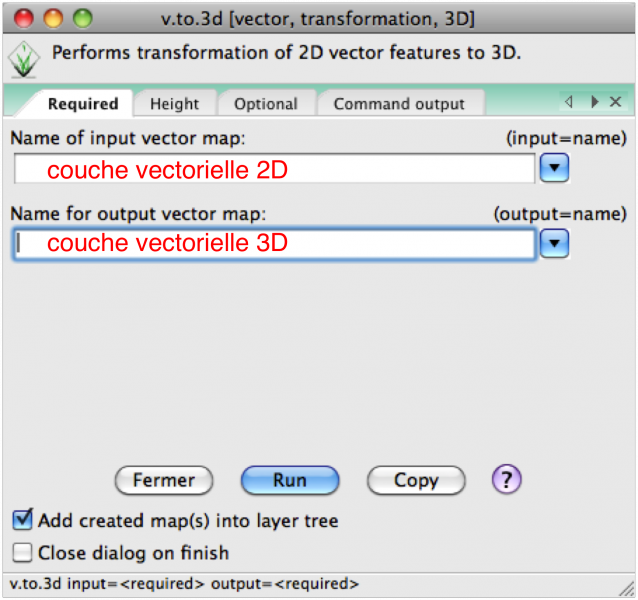
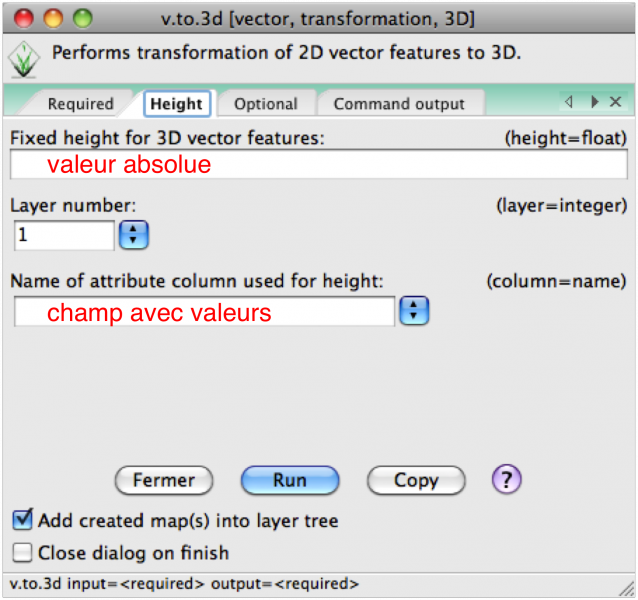
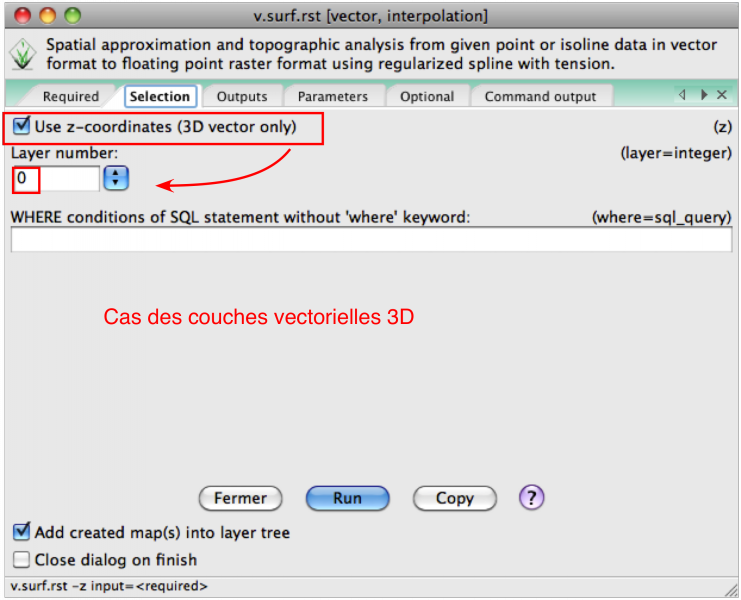
• v.to.3D (menu File/Map type Conversion ou Vector/Map type Conversion) à partir d'un champ de la table d'attributs ou d'une valeur constante:

• v.drape (menu Vector/Develop vector map), à partir d'une surface existante

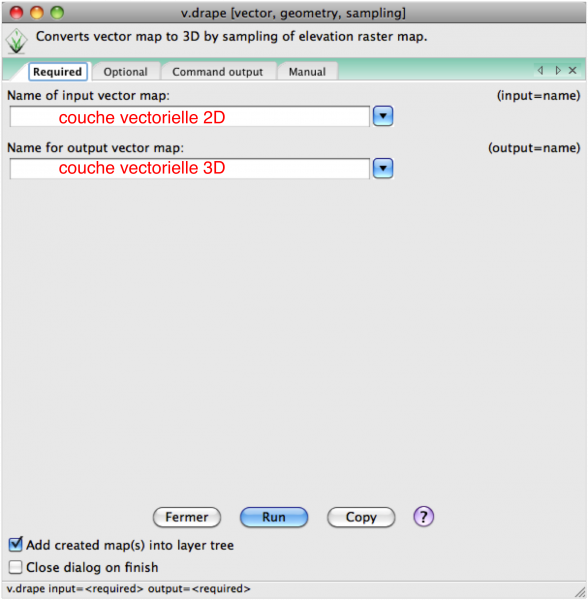
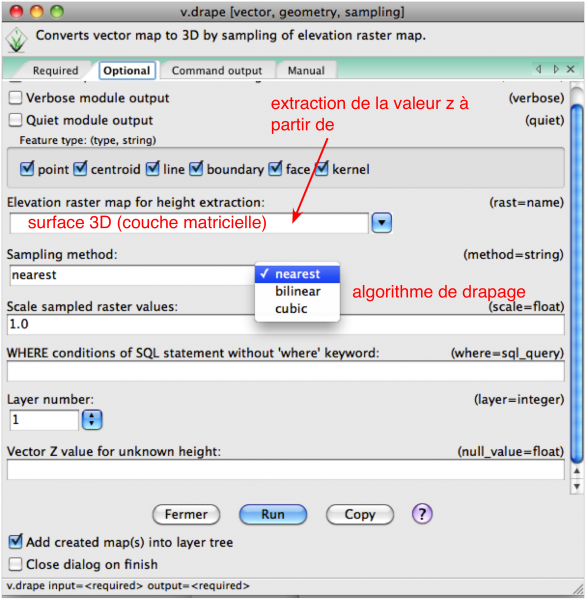
• Si vous avez lu GRASS GIS : géométries, topologies et conséquences pratiques (vecteurs, rasters, volumes), vous comprendrez une des spécificités de GRASS: une couche vectorielle est composée de plusieurs couches (layer 0, layer 1, etc.). Dans le cas d'une couche 3D, la valeur z se trouve dans la couche 0 (layer 0)

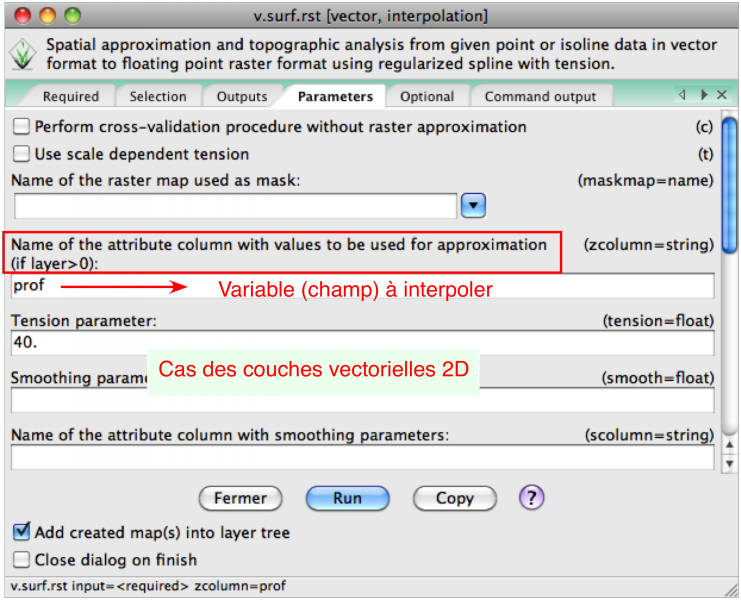
• dans le cas des couches vectorielles 2D, il est toujours possible de spécifier la valeur à interpoler:

Conclusions

Vous êtes maintenant armés pour aborder la suite:

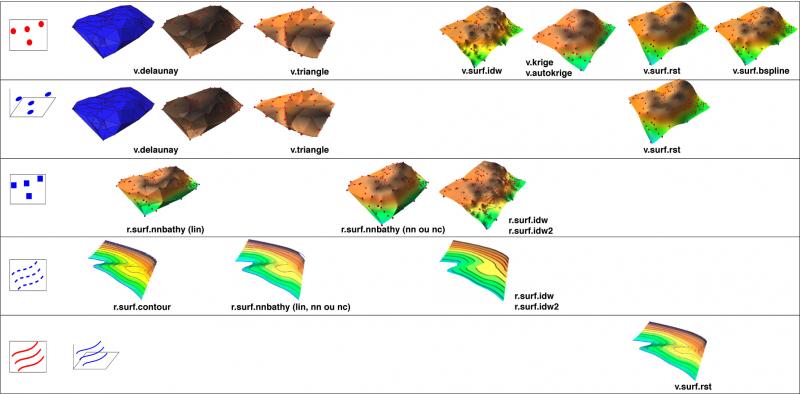
Je vais insister fortement sur le fait qu'il ne faut pas hésiter à regarder l'aide des commandes des modules qui seront utilisés dans la suite. Il y en a qui sont très complexes, avec de nombreuses options qui ne peuvent pas être présentées dans cette introduction générale. Cela évitera des commentaires du genre « ce tutoriel n'est pas assez précis pour répondre à mon problème, car il ne détaille pas les attributs des fonctions ». Et donc, dans la suite:

n'oubliez pas de lire l'aide (onglet Manual) pour comprendre les options (onglets Optionals, Settings ou Parameters) de chaque interface présentée.

et de poser vos questions sur le ForumSIG !

Tous les traitements ont été effectués sur Mac OS X avec GRASS GIS 6.4.1 ou  6.4.2  et Inkscape pour les figures.

Site officiel : GRASS GIS
Autres Liens : GRASS GIS : géométries, topologies et conséquences pratiques (vecteurs, rasters, volumes)
Autres Liens : Grass Gis, ses amis Python et R, ou la puissance d'un shell pas si "ringard" que ça... (traitement des données, géostatistiques and Co.)
Autres Liens : Logiciels SIG, erreurs, incertitudes, propagation des incertitudes ou les grands oubliés dans les traitements courants...
Autres Liens : GRASS GIS pour les experts: 1 - créer son propre module: r.in.rgb (importation directe d'un raster en couleur) en Python avec un menu pour le lancer
Autres Liens : Mac OS X: comment installer un module supplémentaire ("add-on")
Autres Liens : GRASS GIS pas à pas pour les débutants: 8 - les modules d'interpolation spatiale: partitionnement de l'espace, Delaunay (TIN), polygones de Voronoï, algorithmes des plus proches voisinsdébutants: 8 - les modules d'interpolation spatiale: partitionnement d
Autres Liens : GRASS GIS pas à pas pour les débutants: 9 - les modules d'interpolation spatiale: algorithmes avec pondération, inverse de la distance (IDW) et Krigeage géostatistique
Autres Liens : GRASS GIS pas à pas pour les débutants: 10- les modules d'interpolation spatiale: splines régularisées avec tension (RST) et splines bilinéaires et bicubiques avec régularisation de Tykhonov
Autres Liens : GRASS GIS pas à pas pour les débutants: 11- les modules d'interpolation spatiale: traitement des isolignes (courbes de niveau,etc.) et conclusions générales

licence Creative Commons Paternité-Pas d'Utilisation Commerciale-Partage des Conditions Initiales à l'Identique Commerciale 2.0 France