GRASS GIS pas à pas pour les débutants: 8 - les modules d'interpolation spatiale: partitionnement de l'espace, Delaunay (TIN), polygones de Voronoï, algorithmes des plus proches voisins

	Niveau	Débutant
	Logiciels utilisés	GRASS GIS
	Plateforme	Windows | Mac | Linux | FreeBSD

 Il existe deux principaux types de partitionnement d'une variable en régions disjointes à partir des points d'entrée, par polygones et par triangles. Le partitionnement par triangles est celui de Delaunay qui permet de créer un TIN, celui par polygones porte plusieurs noms, polygones de Thiessen , diagramme ou polygones de Voronoï ou mosaïque ou tesselation de Dirichlet.

La couche test sur laquelle les modules seront appliqués (et les sondages, pour les géologues) a été présentée dans la partie 7 de même que les rappels:

n'oubliez pas de lire l'aide (onglet Manual) pour comprendre les options (onglets Optionals, Settings ou Parameters) de chaque interface présentée.

  = couches vectorielles poins ou lignes

  = couches rasters « points» et « lignes»

= couches vectorielles points et lignes 3D

Delaunay et réseaux triangulés irréguliers (TIN)

En entrée:

 

La surface interpolée va passer par les points d'origine, mais les crêtes et les creux peuvent s'étendre au-delà de la valeur maximale et de la valeurs minimale de la variable utilisée.

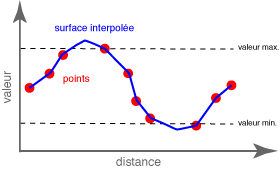
Commande: 

C'est la commande v.delaunay (adaptée par Pavlovsky, 2008) qui est utilisée. Dans le cas de points 2D le résultat sera une couche vectorielle 2D, dans le cas de points 3D (ce qui est le cas ici), le résultat sera une couche vectorielle 3D à faces (voir GRASS GIS : géométries, topologies et conséquences pratiques (vecteurs, rasters, volumes)).

Interface:

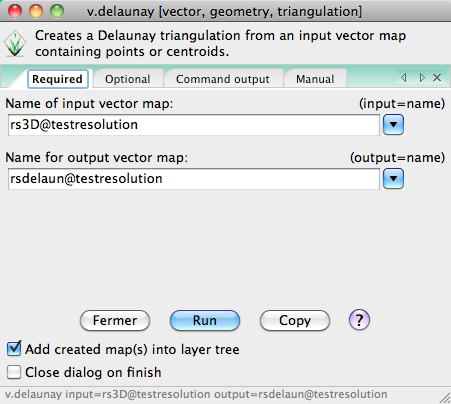
Résultats:

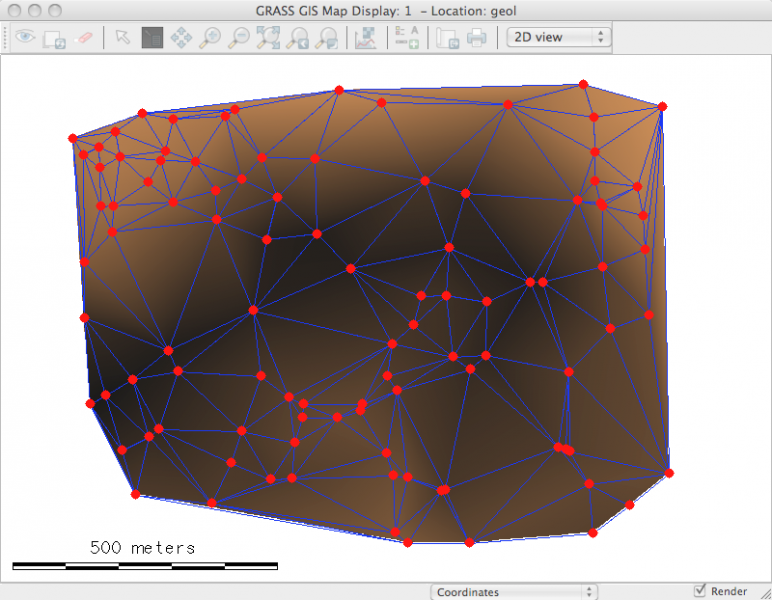
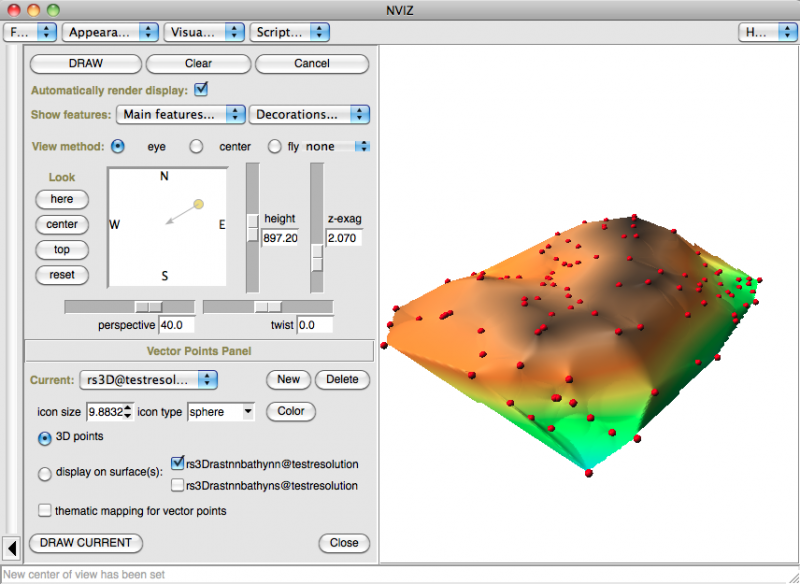
Dans le cas de points 3D comme ici, le résultat est une couche vectorielle 3D de type surfacique (polygone avec faces):

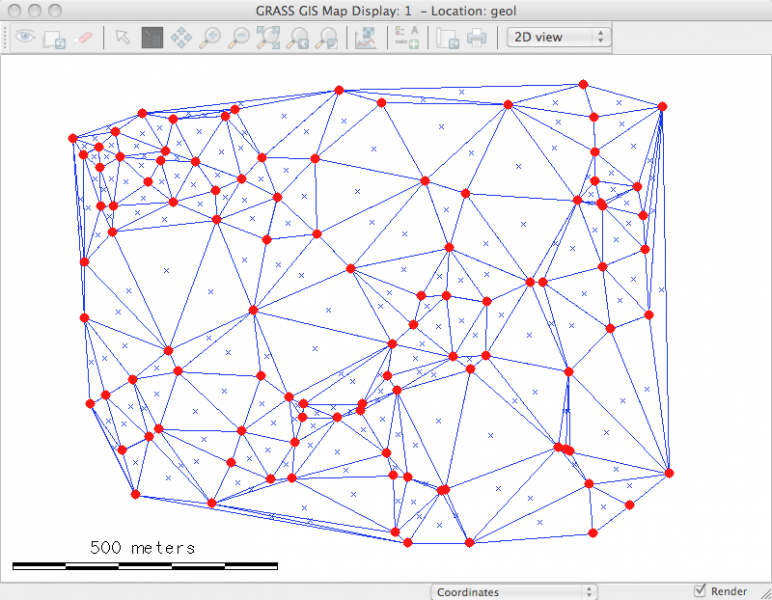
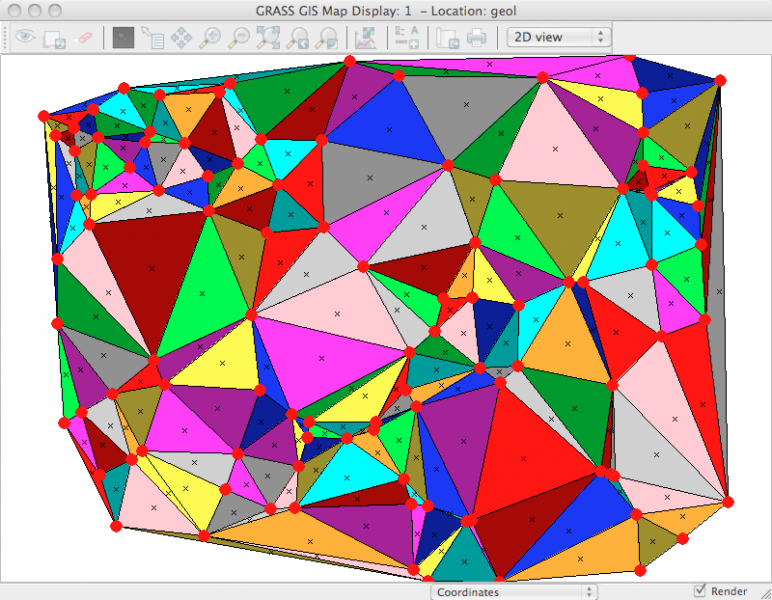
avec couleurs aléatoires ici

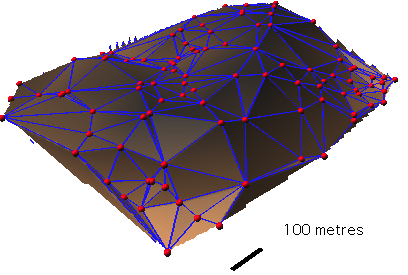
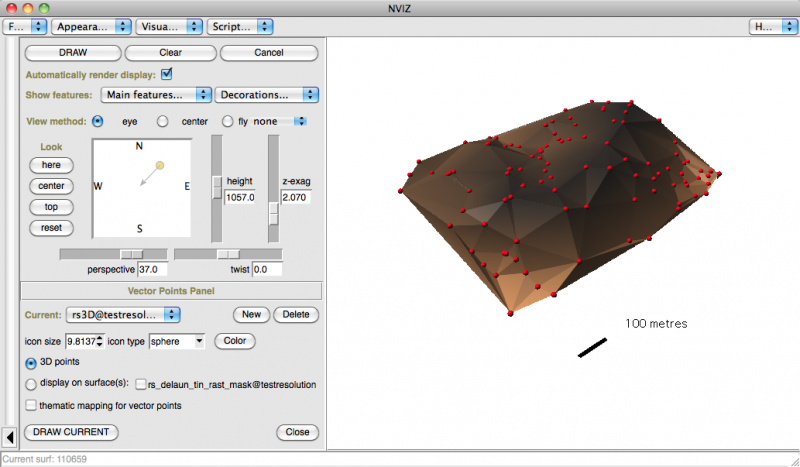
dans nviz (avec les limites des faces ou triangles de Delaunay):

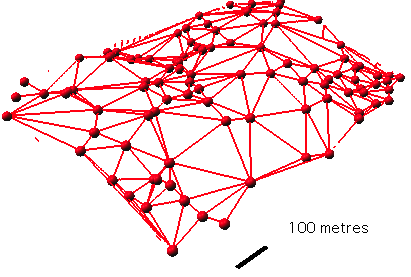
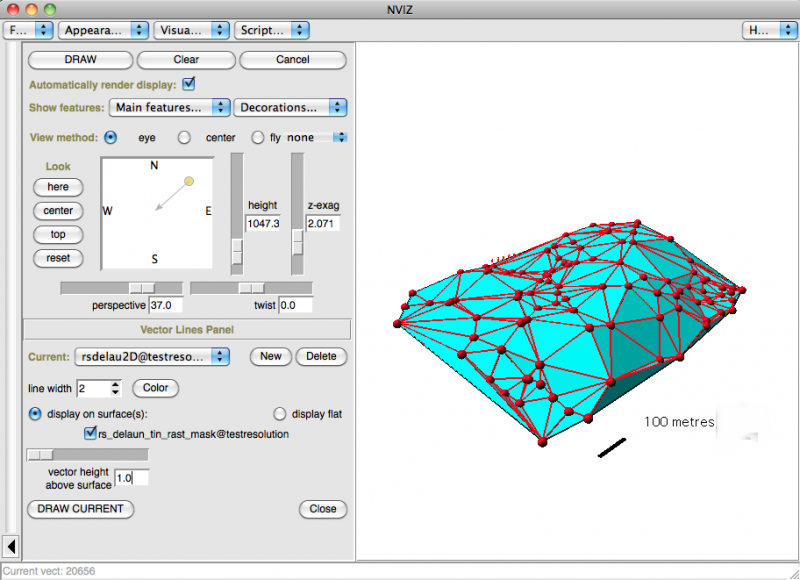
               les limites des triangles de Delaunay             le résultat de v.delaunay est bien un polygone 3D à faces

Pour les géologues (sondages)

C'est une méthode particulièrement adaptée pour le cas qui nous concerne:

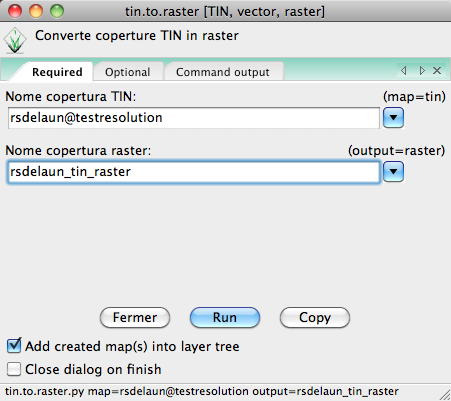
Transformation en surface matricielle (raster):

Cette couche vectorielle peut aussi être transformée en surface matricielle avec, par exemple, le module en Python tin.to.raster.py proposé Antonio Alliegro (digilander.libero.it/antonioall/python_tin2raster.html, en italien) (ici v.to.rast ne marche pas bien). Le processus doit être effectué avec un MASK (voir GRASS GIS pas à pas pour les débutants: 6 - les masques (MASK) et leurs utilisations, rapport avec les régions et l'algèbre des cartes):

Résultats en 2D et avec nviz:

Pour les géologues (sondages):

Module complémentaire -> r.surf.nnbathy:

Parmi ceux présentés dans la première partie nous utiliserons le module r.surf.nnbathy avec l'algorithme lin (linéaire) ou l, basé sur le programme Triangle (www.cs.cmu.edu/~quake/triangle.html)

En entrée:

 

La couche vectorielle point 3D doit préalablement être transformée en couche matricielle 3D (voir la partie 7 de ce thème)

Commande:  

r.surf.nnbathy alg=l input=pts3Draster output=surfacennbathy (ou alg=lin, modifié par moi pour plus de clarté))

Interface:

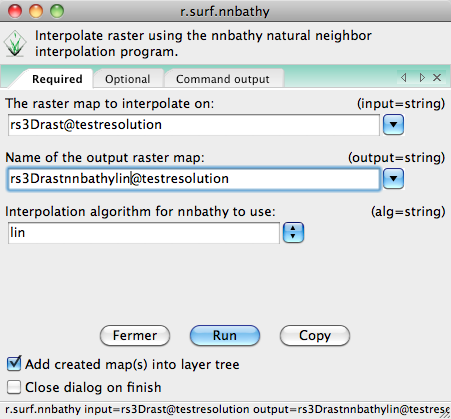
Résultats:

Le résultat est directement une surface matricielle:

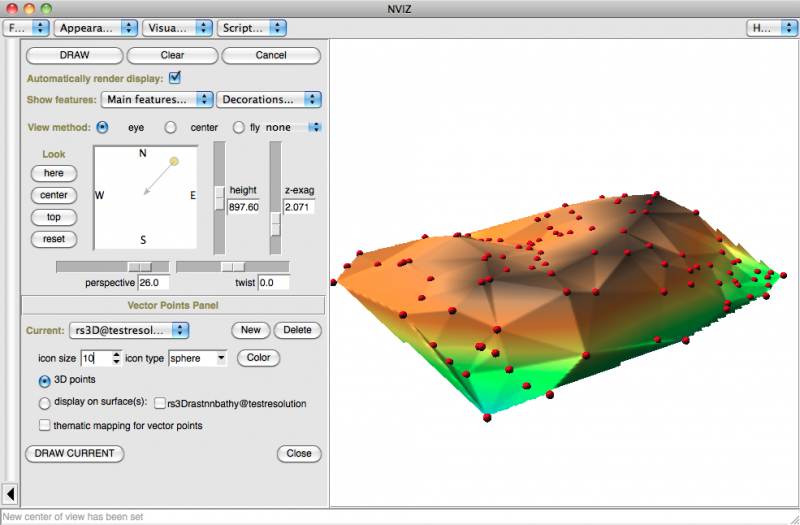
résultat avec r.nnbathy 

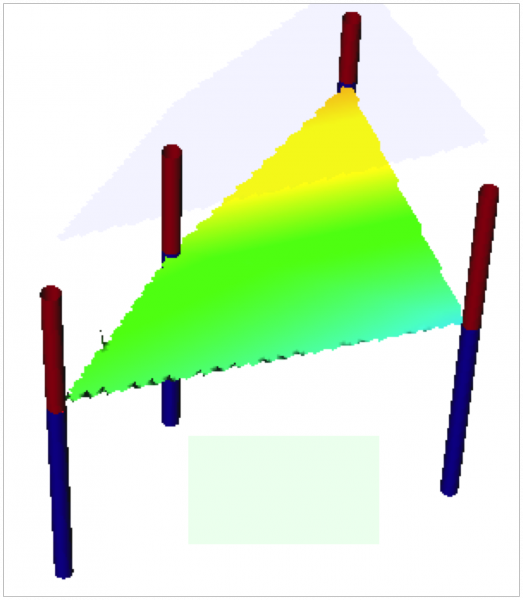
Pour les géologues (sondages)

r.surf.nnbathy permet aussi très facilement de traiter les surfaces des couches recoupées par les sondages:

 

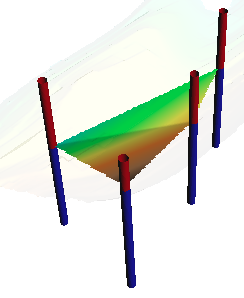
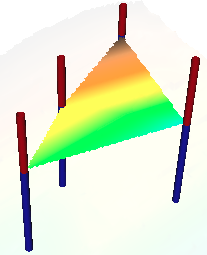
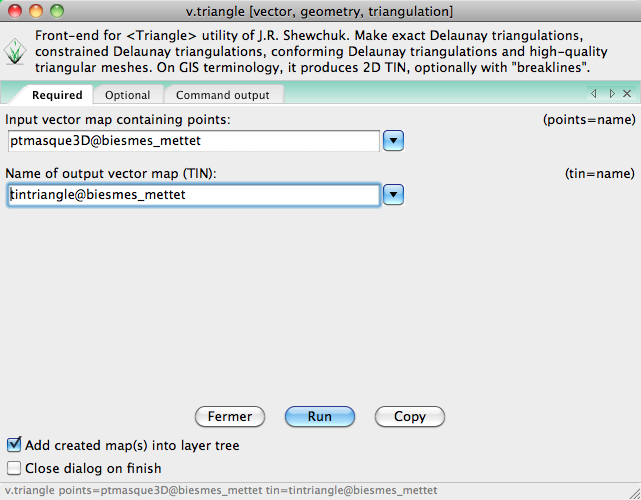
Module complémentaire -> v.triangle = TIN avec lignes de rupture (breacklines) :

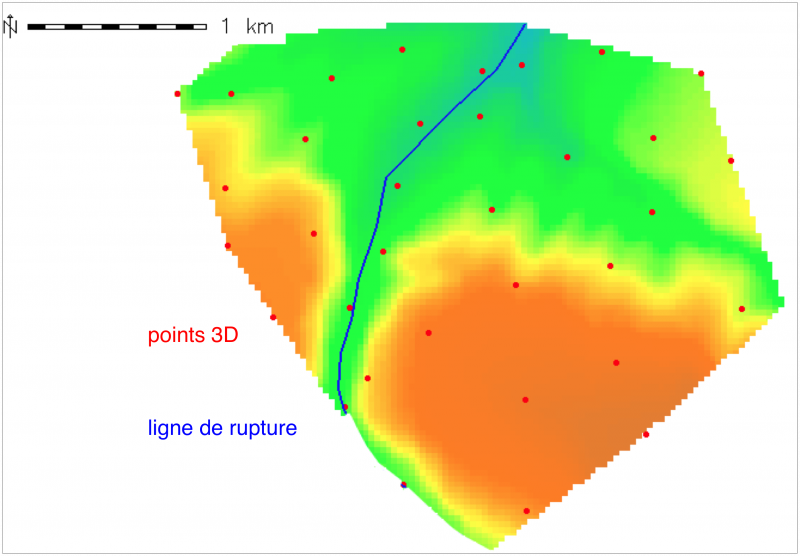
Nous utiliserons ici d'autres données plus favorables à l'existence d'une ligne de rupture (ici vallée sur le DEM SRTM 3 de la NASA) avec la ligne de rupture en bleu et les points à interpoler en rouge (obtenus avec v.to.rast à partir du DEM:

En entrée:

      +     

Il est nécessaire que les deux couches vectorielles (points + ligne(s) de rupture) soient des couches 3D.

Interface:

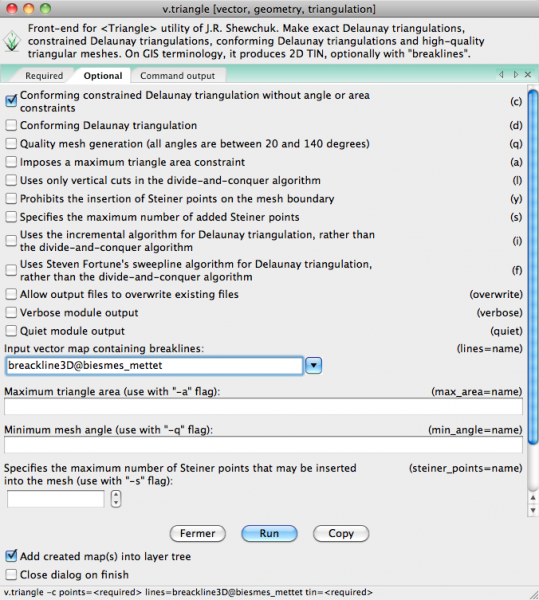
Les options disponibles sont toutes celles du programme Triangle:

Résultats:

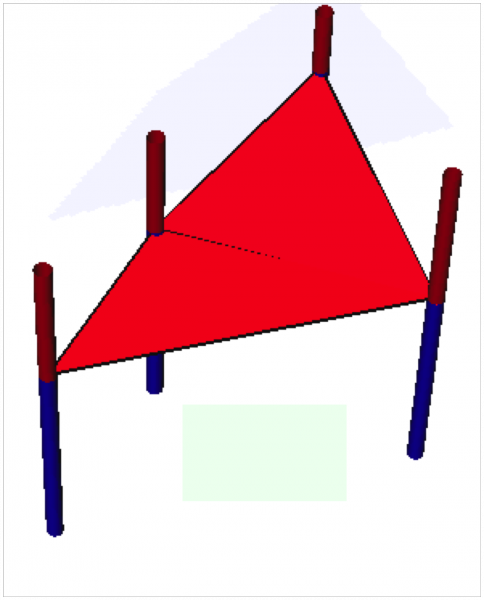
Le résultat (couche vectorielle 3D) de v.triangle (à gauche) comparé avec celui de v.delaunay (à droite):

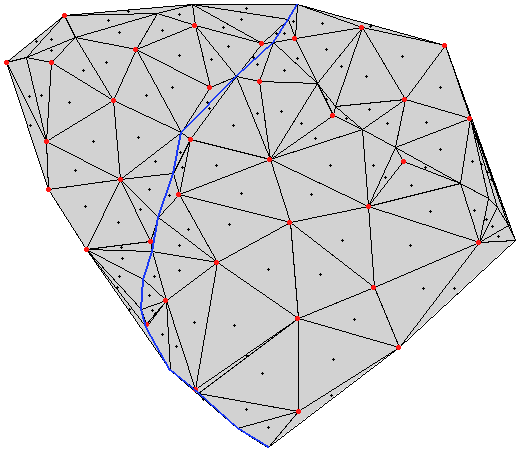
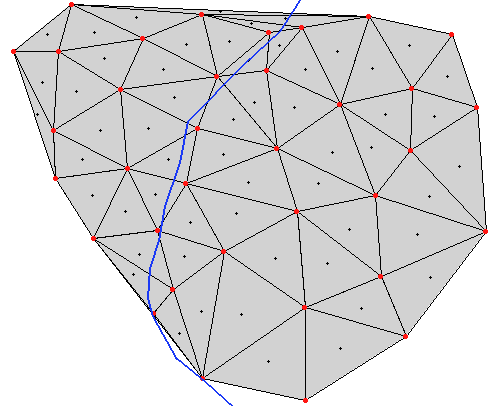
L'ensemble, passé à la moulinette de tin.to.raster.py (avec un MASK), v.triangle, à gauche, et v.delaunay, à droite:

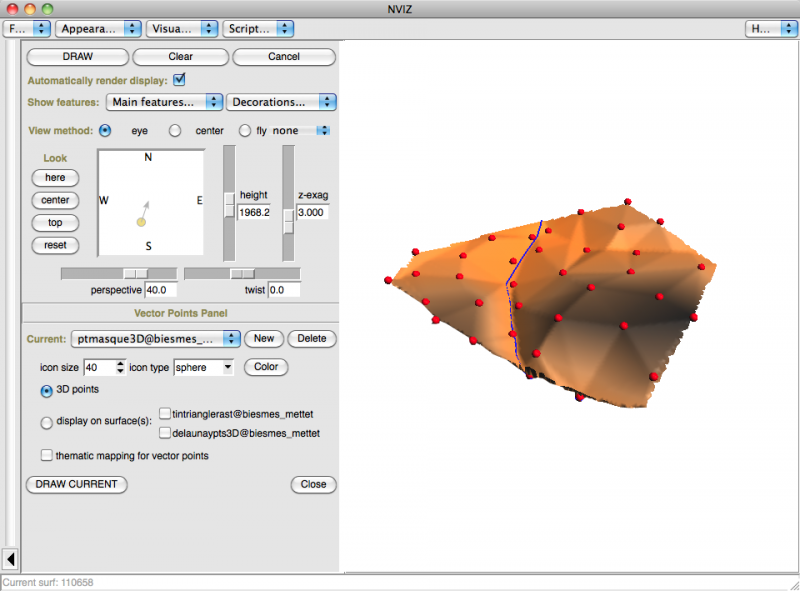
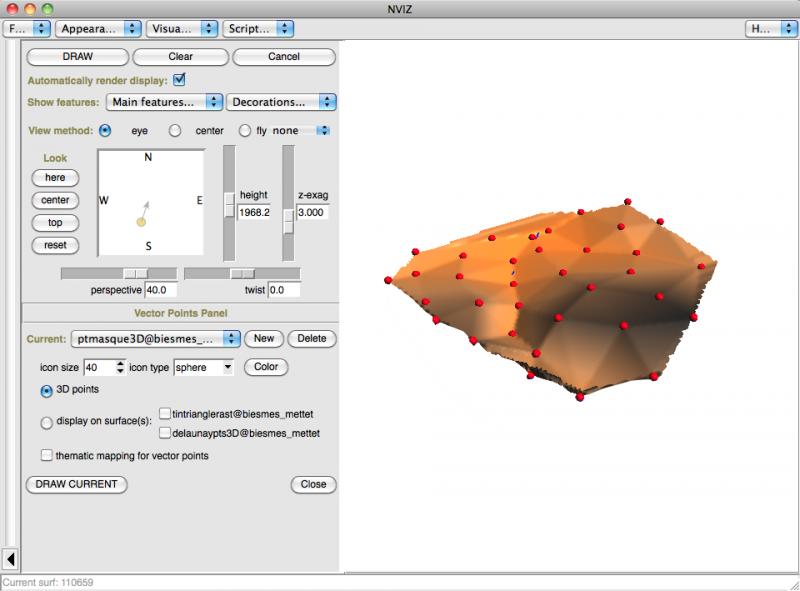
Conclusions

Le principal inconvénient de cette méthode est que la surface n'est pas lissée, avec les angles résultant de la triangulation. Elle dépend aussi de la densité et de la répartition des points de départ. Le grand avantage est qu'elle passe exactement par tous les points traités.

Polygones de Voronoï 

En entrée:

Commande:

v.voronoi

Interface:

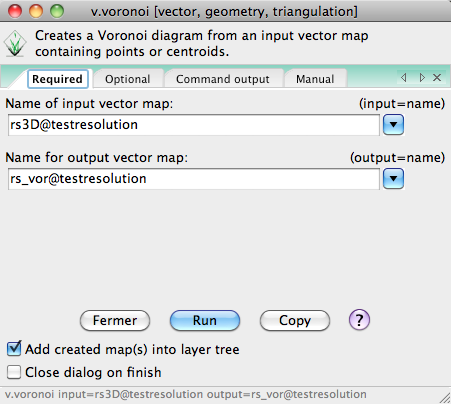
Résultats:

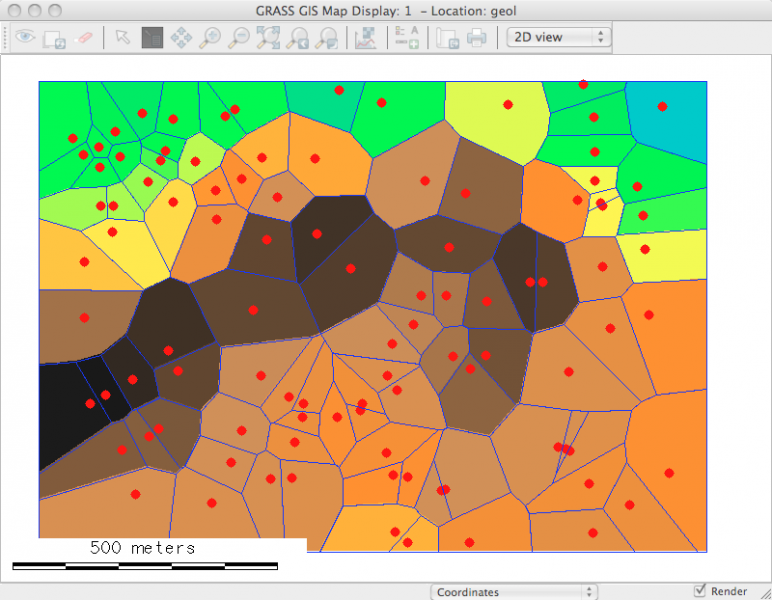
Le résultat est une couche vectorielle 2D de type surface, mais avec les altitudes préservées, ce qui permet de la transformer en couche vectorielle 3D ou en surface matricielle 3D:

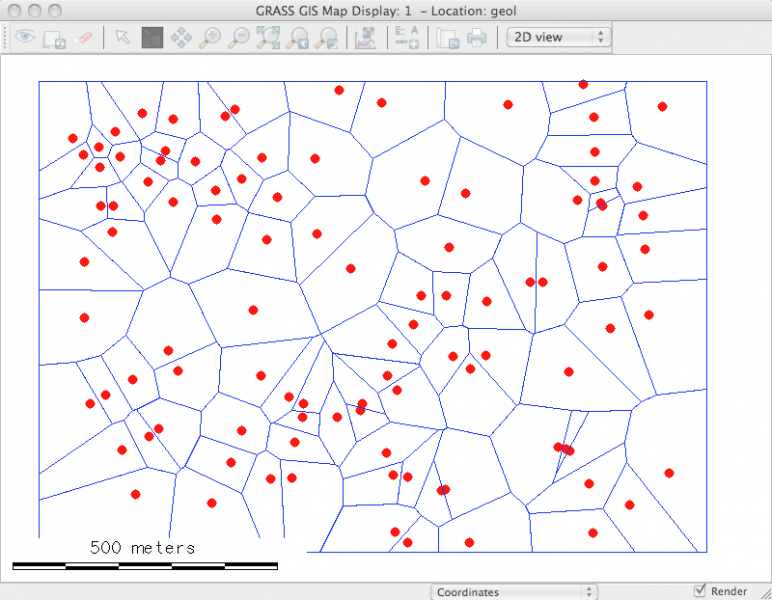
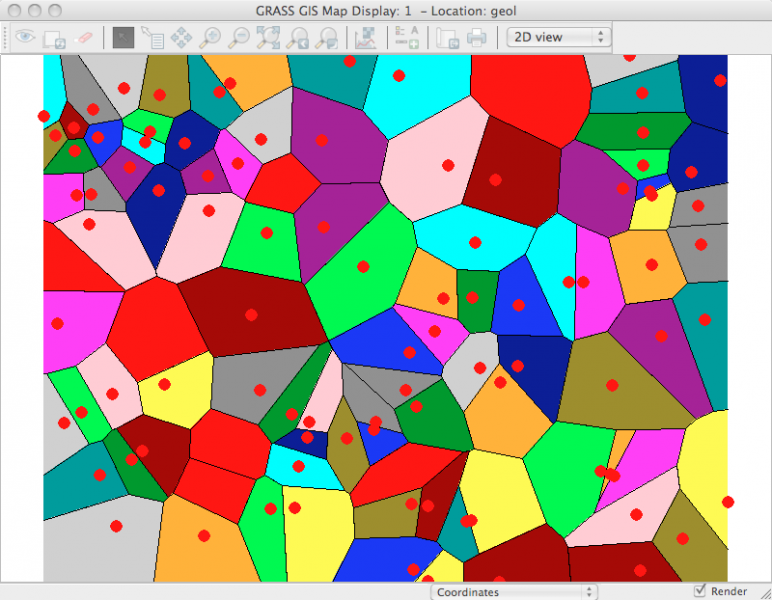
le résultat est bien une couche vestorielle surfacique (avec couleurs aléatoires ici)

Transformation en surface matricielle (raster):

La transformation en surface matricielle 3D se fait toujours avec la commande v.to.rast en tenant compte de la colonne qui contient les altitudes (et ici avec la table de couleurs elevation puisqu'on traite des altitudes):

dans nviz:

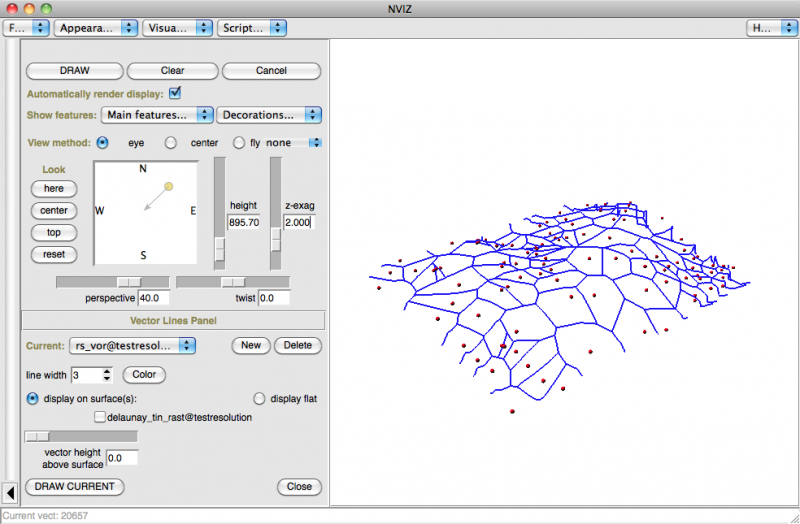
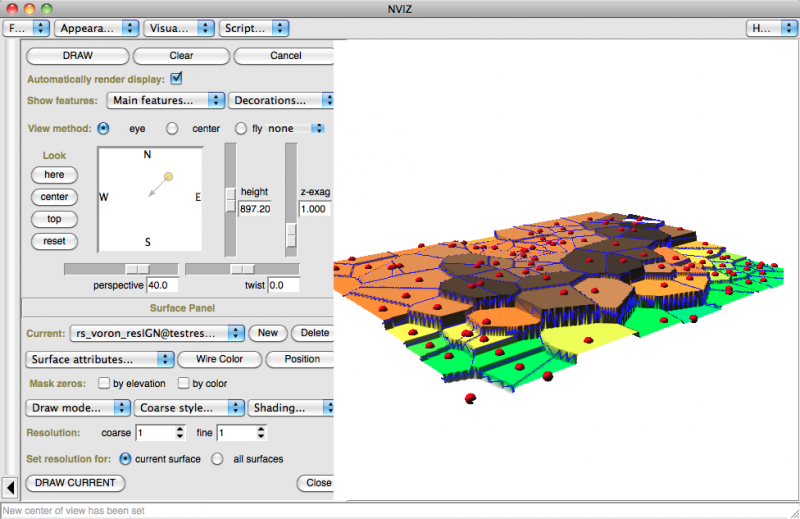
couche vectorielle résultante seule                                                         surface matricielle

Conclusions

Le résultat n'est clairement pas indiqué pour le cas qui nous concerne, il est trop dépendant de la distribution spatiale des points. Cette technique est surtout utilisée dans le cas de valeurs discrètes, non continues. C'est une des méthodes de base dans l'interpolation météorologique et climatique.

Interpolation par l'algorithme des plus proches voisins

Plusieurs autres méthodes se basent sur ce partitionnement de l'espace comme celle des plus proches voisins. La valeur d'un point est attribuée à tous les points localisés dans le polygone de Thiessen ou de Voronoï de ce point. La prévision de la valeur prendra alors la forme d'une moyenne pondérée des valeurs observées (voir moyennes pondérées, sigomatic.blogspot.com/2009/09/plus-proches-voisins.html).

La surface interpolée est étroitement contrôlée par les points  d'origine mais elle ne dépassera pas la valeur maximale et de la valeur minimale de la variable utilisée (du fait de la pondération).

Module complémentaire -> r.surf.nnbathy

En entrée:

Commande:

Cela ne peut être fait qu'avec le module r.surf.nnbathy avec les algorithmes nn (algorithme de Watson pour l'interpolation de Sibson) ou nc (algorithme de Belikov et Semenov pour l'interpolation non Sibsonnienne) basés sur le programme nnbathy et la librairie nn (code.google.com/p/nn-c/)

Interface:

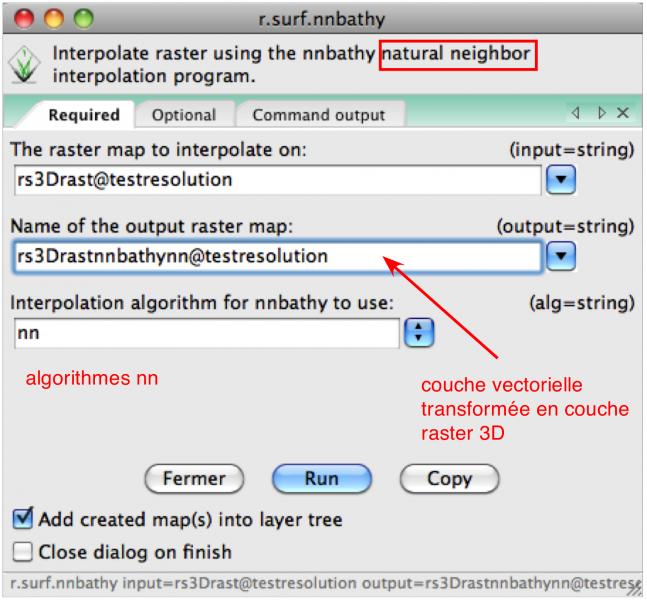
• Résultat

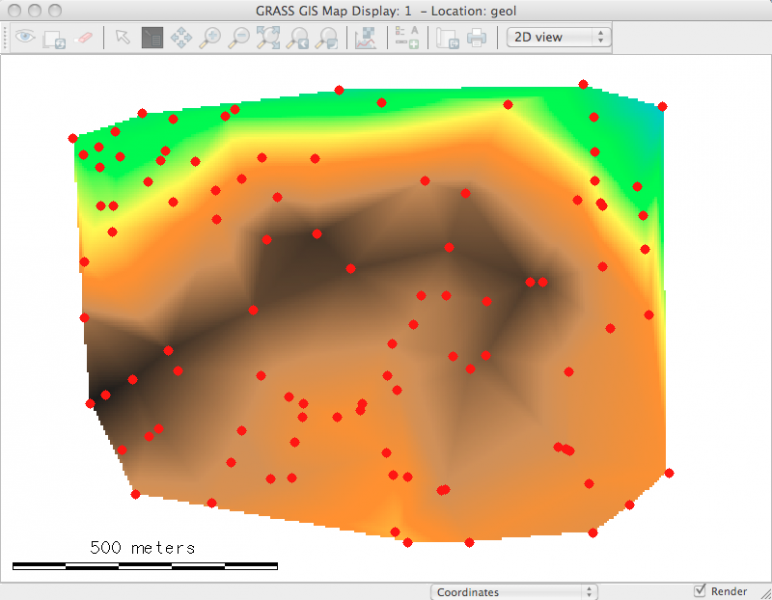
résultats

Conclusions

Il est nécessaire d'avoir le module r.surf.nnbathy. Cette méthode est la plus appropriée lorsque les données traitées sont distribuées suivant une densité inégale.

Tous les traitements ont été effectués sur Mac OS X avec GRASS GIS 6.4.1 ou  6.4.2  et Inkscape pour les figures.

Site officiel : GRASS GIS
Autres Liens : GRASS GIS pas à pas pour les débutants: 6 - les masques (MASK) et leurs utilisations, rapport avec les régions et l'algèbre des cartes
Autres Liens : GRASS GIS pas à pas pour les débutants: 7 - les modules d'interpolation spatiale: introduction, passage d'une couche vectorielle à une couche matricielle (v.to.rast) et d'une couche vectorielle 2D à une d'une couche vectorielle 3D (v.to.3D, v.drape)
Autres Liens : GRASS GIS pas à pas pour les débutants: 9 - les modules d'interpolation spatiale: algorithmes avec pondération, inverse de la distance (IDW) et Krigeage géostatistique
Autres Liens : GRASS GIS pas à pas pour les débutants: 10- les modules d'interpolation spatiale: splines régularisées avec tension (RST) et splines bilinéaires et bicubiques avec régularisation de Tykhonov
Autres Liens : GRASS GIS pas à pas pour les débutants: 11- les modules d'interpolation spatiale: traitement des isolignes (courbes de niveau,etc.) et conclusions générales
Autres Liens : Grass Gis et Paraview: la modélisation géologique 3D pour les démunis, ou les enthousiastes...

licence Creative Commons Paternité-Pas d'Utilisation Commerciale-Partage des Conditions Initiales à l'Identique Commerciale 2.0 France