|
|
|
| Niveau | Débutant |
| Logiciels utilisés |
GRASS GIS |
| Plateforme | Windows | Mac | Linux | FreeBSD |
Après avoir parcouru les modules qui permettent de créer des surfaces à partir de points 2D ou 3D (couches vectorielles ou matricielles), il reste à examiner comment le faire en partant d'isolignes comme des contours ou des courbes de niveau. Des conclusions générales seront enfin présentées.
La couche test sur laquelle les modules ont été appliqués, présentée dans la partie 7 est une couche vectorielle de points. Ici nous allons utiliser une nouvelle couche vectorielle lignes avec des courbes de niveau.

Les rappels restent les mêmes:
n'oubliez pas de lire l'aide (onglet Manual) pour comprendre les options (onglets Optionals, Settings ou Parameters) de chaque interface présentée.
![]()
![]() = couches vectorielles points et lignes
= couches vectorielles points et lignes
![]()
![]() = couches rasters « points» et « lignes»
= couches rasters « points» et « lignes»
![]()
![]() = couches vectorielles points et lignes 3D
= couches vectorielles points et lignes 3D
Les principales méthodes sont détaillées dans grass.osgeo.org/wiki/Contour_lines_to_DEM
Le point de départ
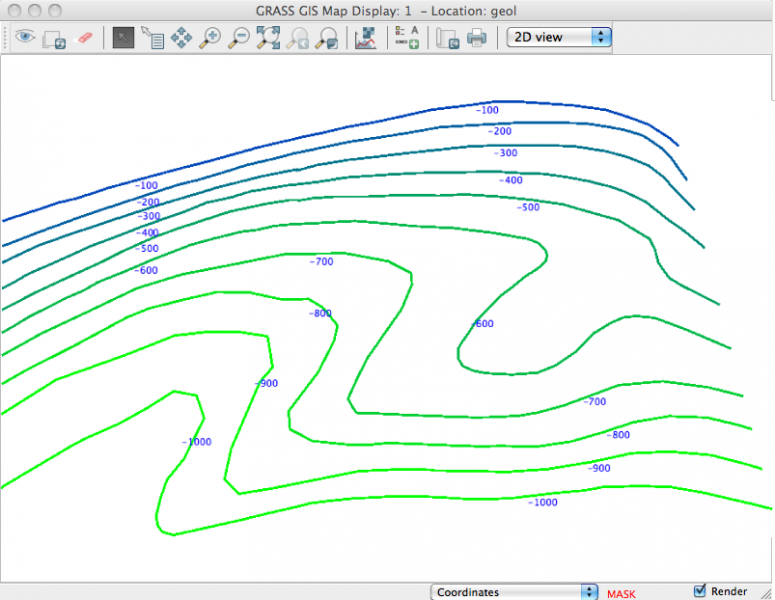
Il s'agit de courbes de niveaux d'une surface de faille qui s'étagent de -1000 à -100m. Vous noterez dans la partie inférieure qu'un MASK est présent pour limiter la surface interpolée à l'emprise des courbes de niveau
r.surf.contour
La couche vectorielle doit d'abord être transformée en couche raster (voir partie 7). Comme ce sont des calculs sur des couches matricielles, la région (surtout le paramètre résolution) est aussi importante à définir, en sus du masque.
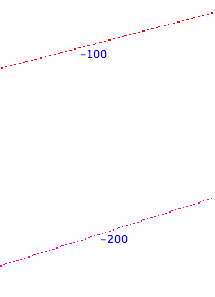
extrait de la couche raster obtenue
Le module n'a pas encore été mis à jour, car il ne peut faire les calculs qu'en nombres entiers avec une interpolation linéaire. La solution provisoire proposée est de passer de mètres en centimètres avec r.mapcalc (couche d'entrée x 100), d'effectuer l'interpolation, puis de revenir en mètres (surface d'interpolation divisée par 100).
En entrée:
Commande:
C'est la commande r.surf.contour
Interface:
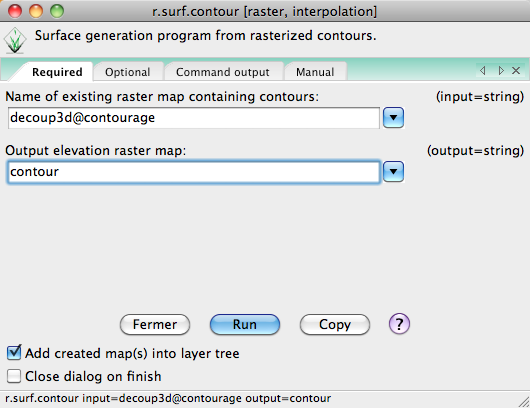
Résultat:
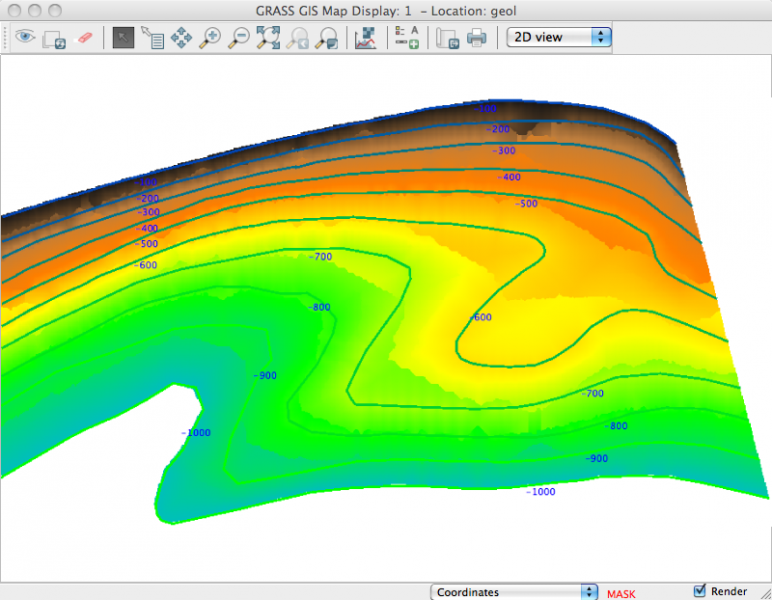
dans nviz:
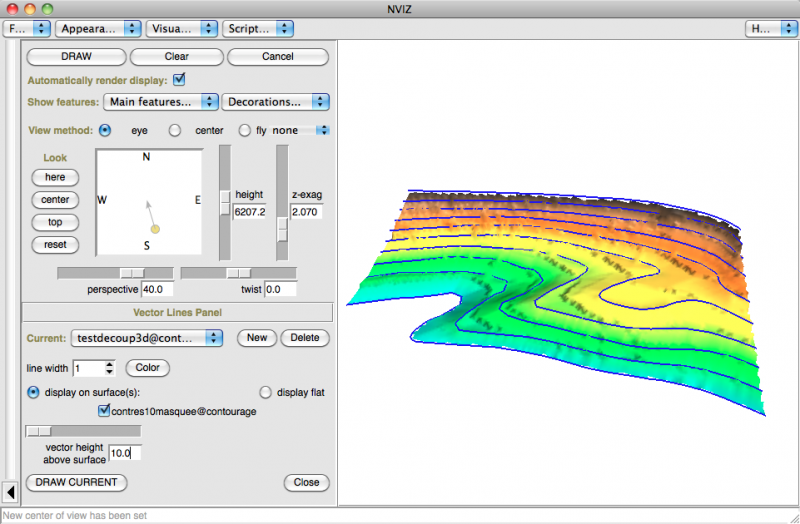
Conclusion:
Le résultat traduit assez bien l'âge et les défauts du module...
r.surf.idw et r.surf.idw2
Ces modules, vus dans la partie 9 peuvent aussi être utilisés avec des couches isolignes transformées en couches matricielles.
En entrée:
Commandes:
r.surf.idw ou r.surf.idw2
Interface:
voir partie 9
Résultat:
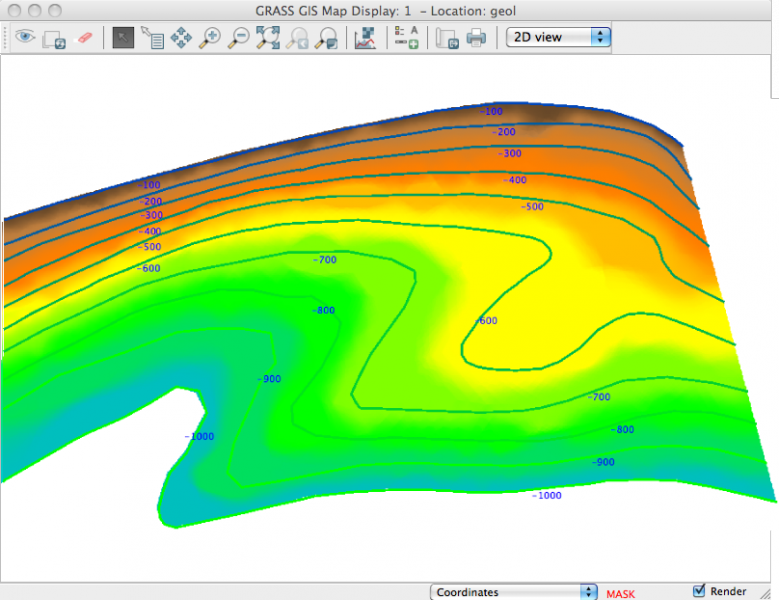
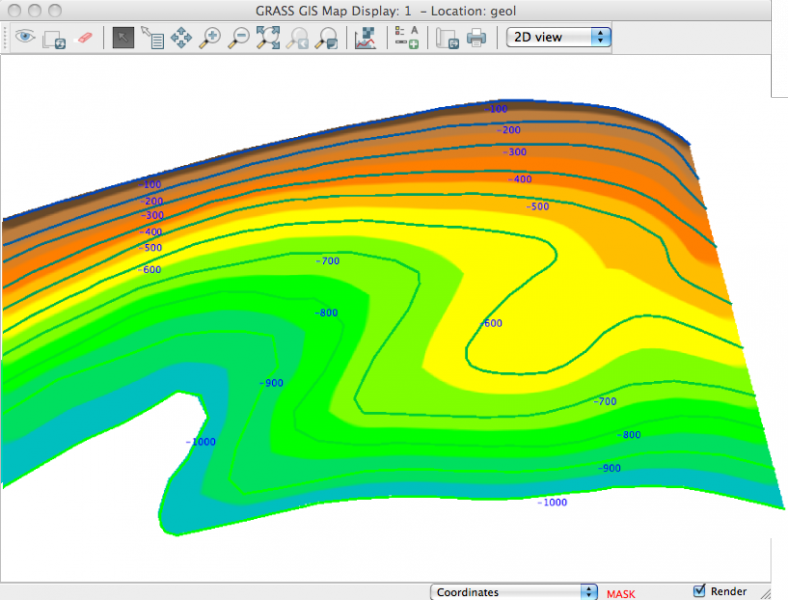
r.surf.idw avec rayon de recherche de 12 pts r.surf.idw2 avec rayon de recherche de 200 pts
dans nviz:
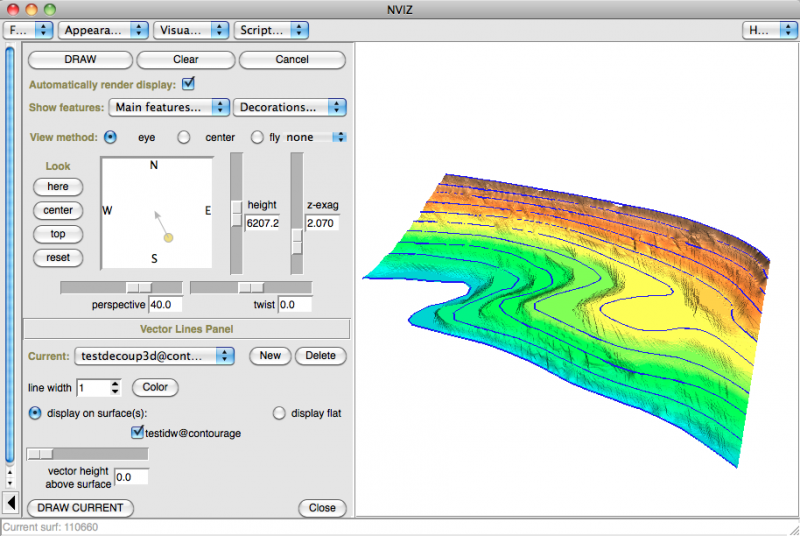
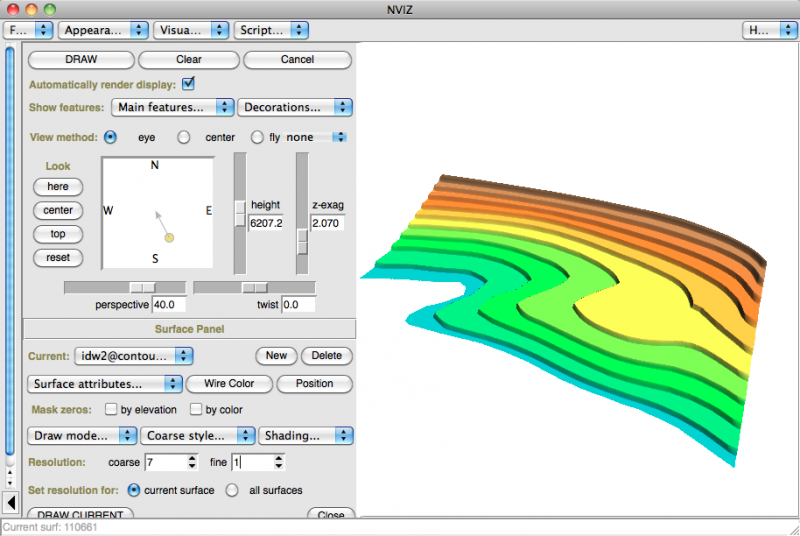
Conclusion:
Ces modules restent très fortement soumis à l'application des paramètres présentés dans la partie 9
module complémentaire: r.surf.nnbathy:
Le module, déjà vu dans les parties 7 et 8 peut aussi être appliqué à des couches isolignes transformées en couches matricielles. Tous les algorithmes lin (=delaunay), nn ou nc (plus proche voisin) peuvent être utilisés. L'agorithme lin est très rapide mais les résultats sont de qualité moindre.
En entrée:
Commandes:
r.surf.nnbathy
Interface:
voir partie 8 et 9
Résultat:
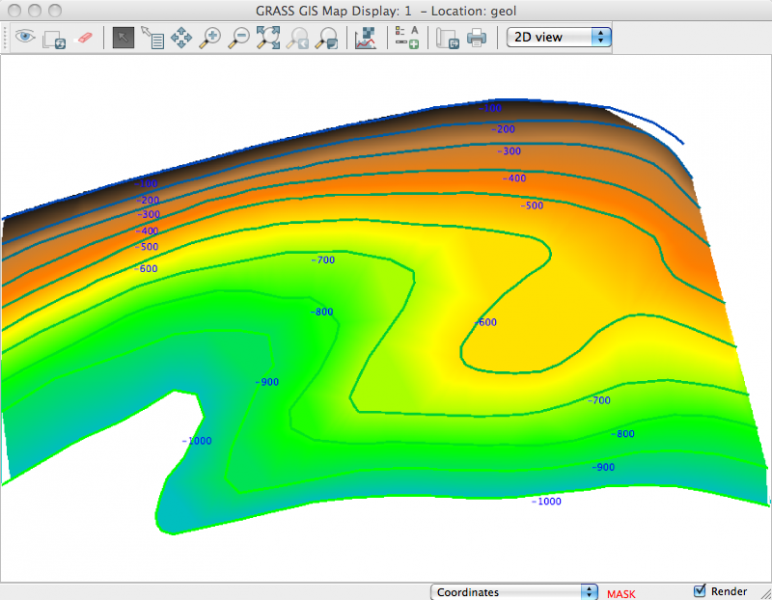
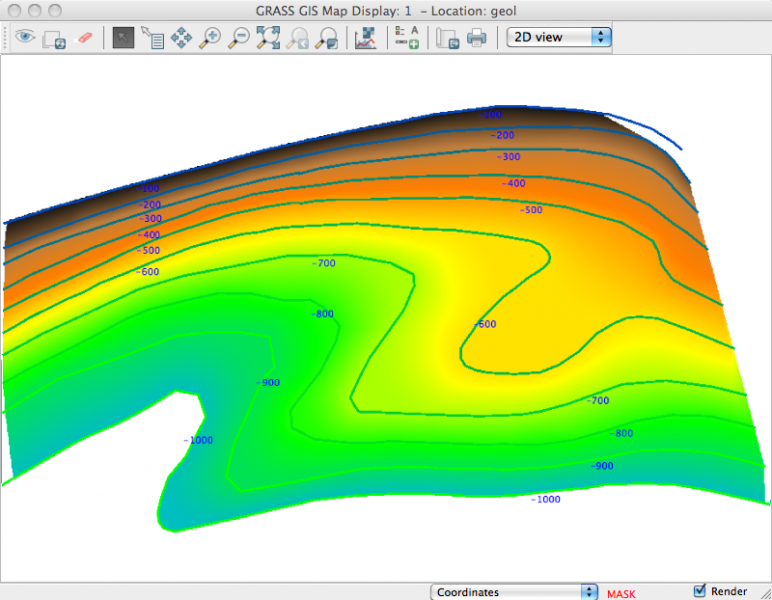
algorithme l (Delaunay) algorithme nn (plus proche voisin)
dans nviz:
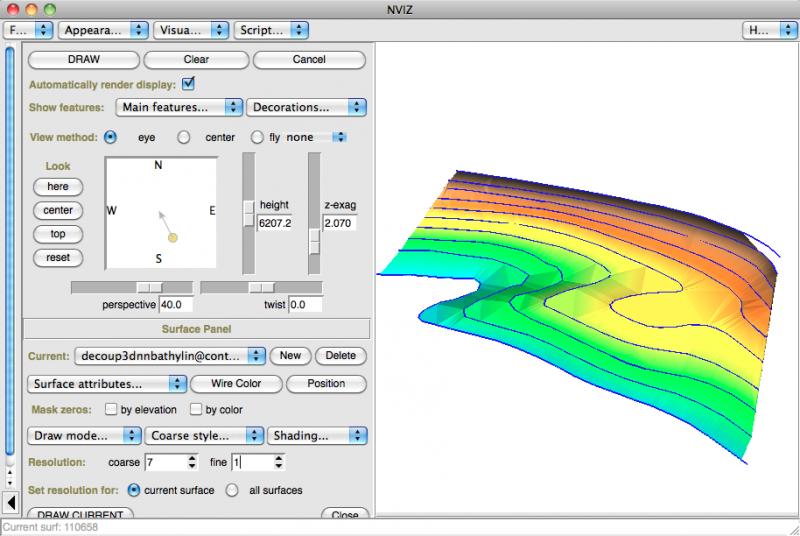
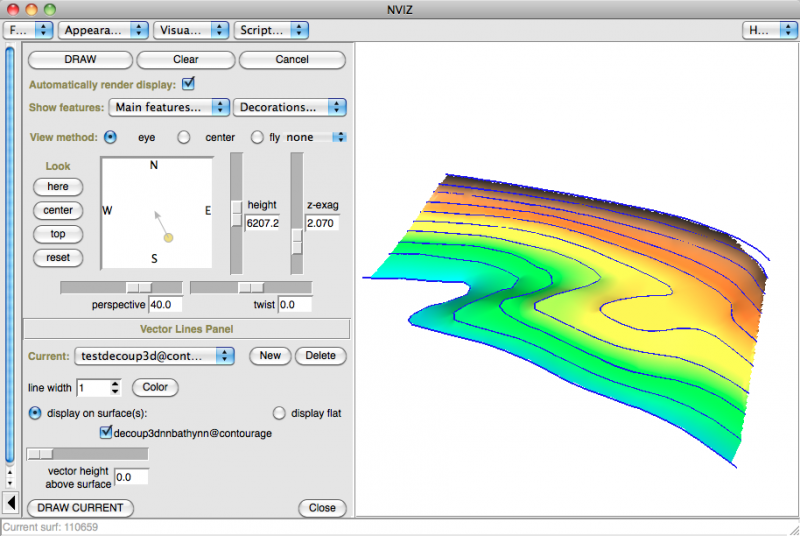
v.surf.rst (splines régularisées avec tension)
Le module a déjà été vu dans la partie 10 sur les splines dans le cas de couches vectorielles points. Il peut être utilisé aussi avec des isolignes.
En entrée:
Commandes:
C'est la commande v.surf.rst
Interface:
voir partie 10
Résultat:
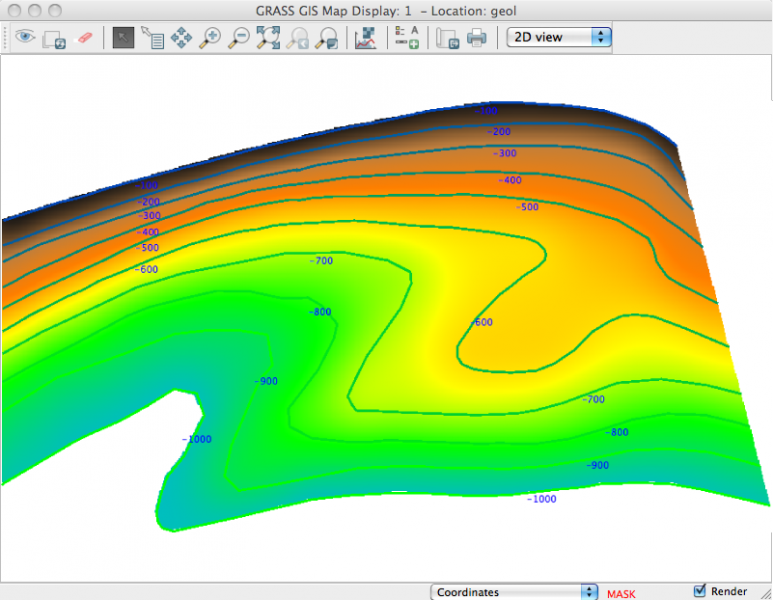
dans nviz
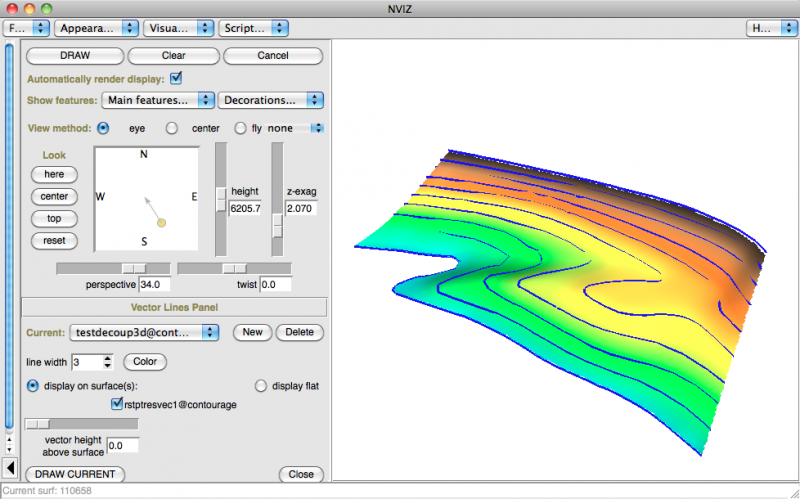
Conclusion:
Le résultat est nettement meilleur, vis-à-vis des courbes de niveau, mais il reste soumis aux nombreuses options de la méthode. Généralement les valeurs par défaut sont suffisantes.
Retour à la case départ : transformation des isolignes en points
Ces isolignes peuvent être transformées en points avec les modules v.to.points (menu Vector/Generate points) ou v.segment (menu Vector/Topology maintenance)
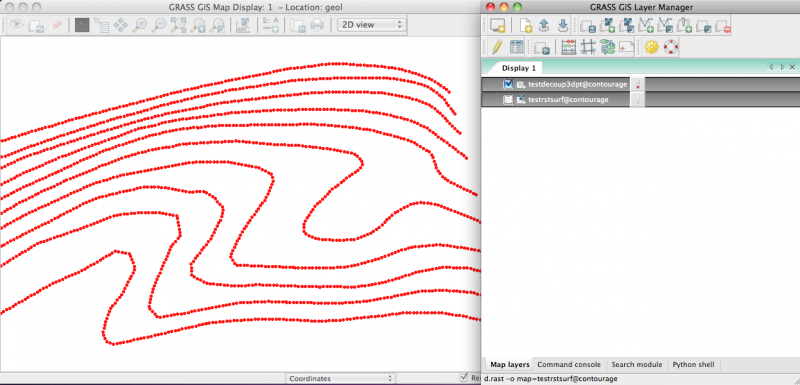
et la boucle est bouclée !
Conclusions générales
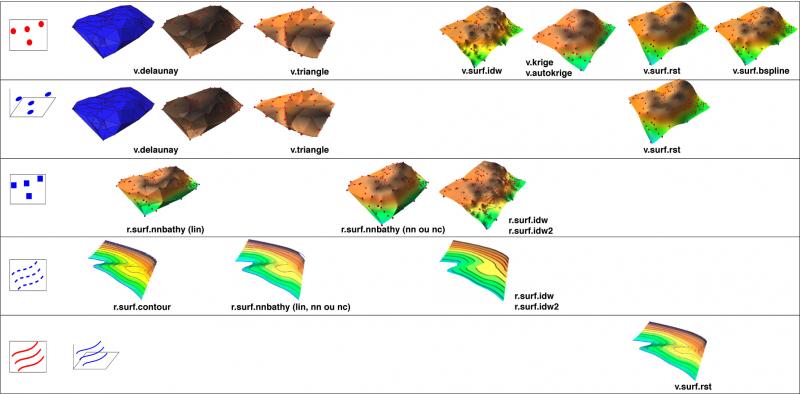
Alors, après cette profusion de surfaces, quelle est la « meilleure » d'entre elles ?
Impossible à dire, vous avez beau être un fervent supporter d'une méthode particulière, rien n'indique qu'elle sera « plus juste » que celles des partisans d'une autre méthode. Elles ont toutes des avantages et des inconvénients et il n'y a pas une méthode parfaite.
Comment alors choisir la meilleure pour vous ?
- la meilleure méthode, est celle qui s'adapte le mieux aux données disponibles, c'est-à-dire qui respecte le mieux l'objectif poursuivi et leur distribution spatiale:
- pour construire une surface géologique, par exemple, je veux une surface qui passe exactement par tous les points utilisés: j'utiliserai donc, soit la méthode par TINs, soit l'interpolation par splines régularisées avec tension (RST) en choisissant les bons paramètres (voir Grass Gis et Paraview: la modélisation géologique 3D pour les démunis, ou les enthousiastes...) et non l'inverse de la distance (IDW) ou le Krigeage géostatistique
- à l'inverse j'utiliserais plutôt ces deux dernières méthodes, si je veux obtenir une surface qui me donne une tendance (comme une modélisation à partir de données géochimiques).
- il est toujours possible d'effectuer les diverses opérations disponibles dans GRASS GIS pour contrôler l'adéquation entre la surface résultante et les données de départ ou d'évaluer les différents résultats obtenus par l'application de différentes méthodes.
- Et hormis cas exceptionnel, à mon avis, il vaut mieux choisir une méthode qui n'implique pas d'hypothèses à vérifier, comme le Krigeage géostatistique, à moins d'être un « as » dans cette matière...
« Getting to know the Kriging method involves delving into the mysterious world of probability and prediction, which, depending on your understanding of statistics, could lead either to years of therapy, or to your Ph.D.» Jochen Albrecht dans www.geography.hunter.cuny.edu/~jochen/GTECH361/lectures/lecture11/concepts/Kriging.htm
J'espère que cette (longue) introduction vous aura donné une idée des forces et des faiblesses de GRASS GIS dans ce domaine (le module de splines régularisées avec tension étant le plus développé). Il ne faut pas non plus hésiter à aller voir ailleurs comme dans SAGA GIS (www.saga-gis.org/en/index.html), malheureusement non disponible sur Mac OS X, qui dispose aussi de son lot de modules d'interpolation spatiale, plus nombreux que dans GRASS, et dont les résultats peuvent être facilement importés. Mais plus vous aurez de résultats...
Car après tout, seul le résultat final compte.
Ah, oui, j'oubliais, la surface originale est un fragment du DEM SRTM 3 de la NASA à partir de laquelle les points aléatoires ont été générés.
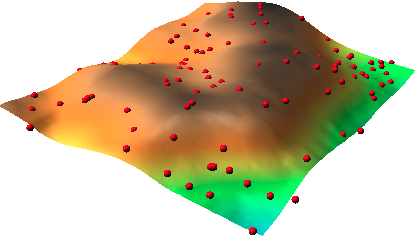
Tous les traitements ont été effectués sur Mac OS X avec GRASS GIS 6.4.1 ou 6.4.2 et Inkscape pour les figures.
 Site officiel :
GRASS GIS
Site officiel :
GRASS GIS  Autres Liens :
Grass Gis et Paraview: la modélisation géologique 3D pour les démunis, ou les enthousiastes..
Autres Liens :
Grass Gis et Paraview: la modélisation géologique 3D pour les démunis, ou les enthousiastes..  Autres Liens :
GRASS GIS pas à pas pour les débutants: 7 - les modules d'interpolation spatiale: introduction, passage d'une couche vectorielle à une couche matricielle (v.to.rast) et d'une couche vectorielle 2D à une d'une couche vectorielle 3D (v.to.3D, v.drape)
Autres Liens :
GRASS GIS pas à pas pour les débutants: 7 - les modules d'interpolation spatiale: introduction, passage d'une couche vectorielle à une couche matricielle (v.to.rast) et d'une couche vectorielle 2D à une d'une couche vectorielle 3D (v.to.3D, v.drape)  Autres Liens :
GRASS GIS pas à pas pour les débutants: 8 - les modules d'interpolation spatiale: partitionnement de l'espace, Delaunay (TIN), polygones de Voronoï, algorithmes des plus proches voisins
Autres Liens :
GRASS GIS pas à pas pour les débutants: 8 - les modules d'interpolation spatiale: partitionnement de l'espace, Delaunay (TIN), polygones de Voronoï, algorithmes des plus proches voisins  Autres Liens :
GRASS GIS pas à pas pour les débutants: 9 - les modules d'interpolation spatiale: algorithmes avec pondération, inverse de la distance (IDW) et Krigeage géostatistique
Autres Liens :
GRASS GIS pas à pas pour les débutants: 9 - les modules d'interpolation spatiale: algorithmes avec pondération, inverse de la distance (IDW) et Krigeage géostatistique  Autres Liens :
GRASS GIS pas à pas pour les débutants: 10- les modules d'interpolation spatiale: splines régularisées avec tension (RST) et splines bilinéaires et bicubiques avec régularisation de Tykhonov
Autres Liens :
GRASS GIS pas à pas pour les débutants: 10- les modules d'interpolation spatiale: splines régularisées avec tension (RST) et splines bilinéaires et bicubiques avec régularisation de Tykhonov 
licence Creative Commons Paternité-Pas d'Utilisation Commerciale-Partage des Conditions Initiales à l'Identique Commerciale 2.0 France

Commentaires
tutoriel Grass gis gps
accès au menu (onglets) pour saisie des données.
Poster un nouveau commentaire