Logiciels SIG, erreurs, incertitudes, propagation des incertitudes ou les grands oubliés dans les traitements courants...

Nous utilisons tous les logiciels SIG pour traiter les données spatiales à l'aide de processus et de calculs divers à partir des données d'entrées pour obtenir des résultats dérivés. Toutes les fonctions permettant de les effectuer sont implémentées sous forme de multiples boutons ou menus dans nos logiciels et la majorité d'entre nous les utilisent sans se poser trop de questions, bien contents d'obtenir des résultats satisfaisants à leurs yeux.

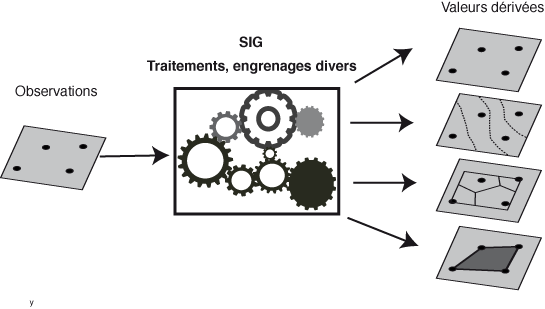
Or aucune carte ou aucune donnée de base n'est malheureusement exempte d'erreur (quantitative et/ou qualitative).  L'estimation de ces erreurs est appelée incertitude (les coordonnées d'un point obtenues par un GPS, par exemple, ont toujours un certain degré d'incertitude lié à divers paramètres, de plus cette incertitude est variable dans le temps).

On devine intuitivement que ces incertitudes vont se propager dans les divers traitements qui vont être effectués. Or lorsqu'une mesure initiale est utilisée pour obtenir la valeur d'une autre grandeur par l'intermédiaire d'une formule, d'une fonction, d'un traitement, il nécessaire de savoir déterminer la valeur estimée, mais aussi l'incertitude induite. C'est ce qu'on appelle la propagation des incertitudes ( fr.wikipedia.org/wiki/Propagation_des_incertitudes).

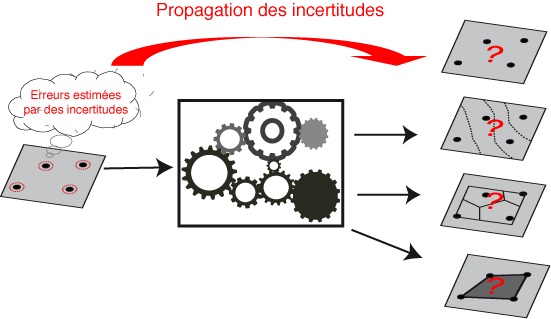
La figure ci-dessus illustre le cas des vecteurs, mais c'est tout aussi vrai dans le cas des traitements ou de la création des  rasters, des grilles ou des MNT.

C'est le domaine d'étude de la métrologie (fr.wikipedia.org/wiki/M%C3%A9trologie), qui est la science des mesures et ses applications, avec des méthodes et même des normes (comme le GUM, « Guide pour l’expression de l’incertitude de mesure »). Ses domaines d'application sont très vastes. Plus simplement, cette propagation est aussi utilisée dans tous les domaines scientifiques où il y a des mesures et des calculs à partir de ces mesures. C'est une notion fondamentale en sciences:

« Étant donné les erreurs dans les données de départ, quelle est l'ampleur des erreurs dans le (s) résultat (s) ? »

Cet aspect est rarement mis en évidence dans le monde des logiciels SIG où l'on se contente généralement de « pousser sur un bouton » pour obtenir un résultat que l'on accepte, sans aller plus loin.

Un simple exemple suffit pourtant à expliquer son importance. Un Sigiste qui désire calculer la surface d'un polygone va utiliser la fonction de son logiciel qui va lui donner un résultat apparemment très précis (généralement avec beaucoup de décimales, ça fait bien). Pourtant la réalité est moins rose...

Examinons le cas d'un rectangle ou d'un carré dont la surface doit être calculée à partir d'une longueur et d'une largeur, avec des incertitudes, ou à partir des coordonnées des sommets, toujours avec des incertitudes. Si le résultat de ce calcul a un certain intérêt économique, comme le calcul de primes en fonction de cette surface, on conçoit tout de suite l'importance cruciale de cette propagation des incertitudes et de la métrologie :

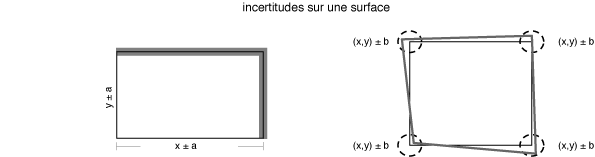
Le résultat devrait donc idéalement être fourni avec un intervalle de confiance. Que faire dans ce cas puisqu'aucun logiciel SIG à l'heure actuelle ne permet de tels calculs ?

Une solution serait de se dire, réduisons ces erreurs quantitatives (mesure, valeur d'un attribut) et/ou qualitatives (valeur d'un attribut) au départ, mais c'est pratiquement impossible (les erreurs sont, par définition, inconnues, sinon elles pourraient être éliminées facilement). Il est en effet nécessaire d’identifier toutes les causes possibles d’erreurs qui pourraient influencer la mesure.

Les questions à se poser sont donc :

• Quelles erreurs, quel type d'erreurs sont présents dans les données de départ ?
• Comment les visualiser, les identifier ?
• Comment les traiter ?

N'étant ni métrologue, ni statisticien, mais un simple scientifique, je vais essayer de vous présenter le sujet de manière intuitive, sans formules mathématiques (pourtant nécessaires). Dans mon domaine, la géologie, nous sommes pratiquement obligés d'en tenir compte et de vivre avec. J'illustrerai l'application de deux des méthodes avec Python, la simulation de Monte-Carlo, et l'approximation de Taylor avec le magnifique module uncertainties d'Éric Lebigot, que je remercie pour l'aide qu'il m'a apportée (" Uncertainties: a Python package for calculations with uncertainties", Eric O. LEBIGOT,  packages.python.org/uncertainties).

Pour ceux qui désireraient aller plus loin dans les mathématiques impliquées dans le sujet, je conseille la lecture de "The Mathematics of GIS, Kainz, W., 2010 (Version 2.1) disponible à homepage.univie.ac.at/wolfgang.kainz/Lehrveranstaltungen/15th_Nordic_Summer_School/The_Mathematics_of_GIS_Draft.pdf

Études consacrées au sujet

Avant d'entamer le sujet, signalons que cet aspect a été surtout étudié depuis les années 1990 et a fait l'objet de nombreuses publications scientifiques, certaines très importantes :

quelques livres ou chapitres de livres :

• "Error Propagation in Environmental Modelling with GIS", Heuvelink, G.B.M.,1998, Taylor & Francis. (www.amazon.com/Propagation-Environmental-Modelling-Research-Monographs/dp/074840743X/ref=sr_1_1)
• "Analysing uncertainty propagation in GIS: why is it not that simple?",Heuvelink, G.B.M. 2002 dans Foody, G.M.  & Atkinson, P.M., Editeurs, Uncertainty in Remote Sensing and GIS, Wiley. (www.amazon.com/Uncertainty-Remote-Sensing-Giles-Foody/dp/0470844086/ref=sr_1_1)
• "Uncertainty in Geographical Information", Zhang J.X.  & Goodchild M.F.,2002,Taylor and Francis; (www.amazon.com/Uncertainty-Geographical-Information-Monographs-Geographic/dp/0415243343/ref=sr_1_1)
• "6.6 Error propagation in spatial data processing", 2004, Rolf A. de By, éditeur, dans Principles of Geographic Information Systems An introductory textbook,  ITC Educational Textbook Series
• "Models of uncertainty in spatial data", Fisher, P.F. 2005 dans Longley P.A., Goodchild M.F., Maguire D.J. & Rhind D.W. (éditeurs), dans Geographical Information Systems: Principles, Techniques, Management and Applications (abridged edition), Wiley
• "Propagation of error in spatial modelling with GIS", Heuvelink, G.B.M., 2005 dans Longley P.A., Goodchild M.F., Maguire D.J. & Rhind D.W. (éditeurs), Geographical Information Systems: Principles, Techniques, Management and Applications (abridged edition), Wiley.
• "6 : Uncertainty" dans Longley, P.A, Goodchild, M.F., Maguire, D., Rhind, D.W., 2005, Geographical Information Systems and Science, 2nd Edition, Wiley. (www.amazon.com/Geographic-Information-Systems-Science-Longley/dp/047087001X/ref=sr_1_2)
• "Modeling Uncertainty in the Earth Sciences", Caers, J, 2011, Wiley-Blackwell. (www.amazon.com/Modeling-Uncertainty-Earth-Sciences-Caers/dp/1119992621/ref=sr_1_1)

ainsi que dans le nouveau livre collaboratif réalisé par le chapitre hispanique de  l'OSGeo:

• Les chapitres 7.5: Detección y medición de errores, 7.6; Propagación de errores y modelación del error et 7.7: Gestion de errores dans Olaya, V., 2011(version 1), "Systema de Information Geographica", disponible à wiki.osgeo.org/wiki/Libro_SIG   (sous licence Creative Common)

en géostatistique :

• "Geostatistics: Modeling Spatial Uncertainty", Chiles, J. & Delfiner, P., 1999, Wiley. (www.amazon.com/Geostatistics-Modeling-Uncertainty-Probability-Statistics/dp/0471083151/ref=sr_1_1)

de nombreux articles disponibles sur Internet comme :

• "Uncertainty Propagation in GIS", Heuvelink, G.B.M.,1998 disponible à www.ncgia.ucsb.edu/giscc/units/u098/u098.html.
• "Assessing the Uncertainty Resulting from Geoprocessing Operations", Krivoruchko K. & Gotway Crawford C. A, 2003 disponible à gis.uml.edu/abrown2/epi/GA/bib/assessing-uncertainty.pdf

des sites Internet comme :

• spatial-accuracy.org/ avec notamment www.spatial-accuracy.org/workshopSUP

et de nombreux articles parus dans des revues scientifiques comme  ceux publiés en 2004 par Leung, Y., Ma, J.-H.  et  Goodchild, M. F. dans la revue Journal of Geographical Systems (www.springerlink.com/content/1435-5930/6/4/) :

• "A general framework for error analysis in measurement-based GIS Part 1: The basic measurement-error model and related concepts", V. 6, N. 4, pp. 325-354
• "A general framework for error analysis in measurement-based GIS Part 2: The algebra-based probability model for point-in-polygon analysis", V. 6, N. 4, pp. 355-379
• "A general framework for error analysis in measurement-based GIS Part 3: Error analysis in intersections and overlays", V. 6, N. 4, pp. 381-402
• "A general framework for error analysis in measurement-based GIS Part 4: Error analysis in length and area measurements", V. 6, N. 4, pp. 403-428

sans parler des articles plus spécialisés...

Identification des erreurs

Qu'entend-on par erreur ?

Elle peut être définie comme la différence entre la réalité et notre perception de la réalité (pour autant qu'elle existe, qu'elle ait un sens clairement défini).

Par exemple, voici l'illustration d'une erreur dans le cas de la localisation d'une observation :

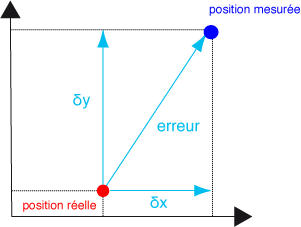
Nous ne discuterons pas ici des sources d'erreurs, quantitatives et qualitatives, des erreurs systématiques ou aléatoires (fr.wikipedia.org/wiki/Erreur_%28m%C3%A9trologie%29). Dans le domaine géospatial, elles sont explicitées dans les divers ouvrages cités.

En pratique, il est toujours possible de mesurer l'erreur finale en analysant les écarts entre les observations de départ et les résultats obtenus par diverses méthodes :

• les indicateurs d'écart entre valeurs observées et les valeurs calculées (MSE, erreur quadratique  moyenne, moyenne des carrés des résidus ou erreur type RMSE (root-mean-square error), etc. (voir  www.jybaudot.fr/Stats/indicecarts.html), utilisés notamment pour évaluer le géoréférencement d'un raster.
• diverses techniques de régression;
• la géostatistique (krigeage, etc.);
• les analyses statistiques multivariées;
• etc.

Illustrons un exemple réel de calcul du RMSE entre deux séries de points, dont l'une résulte d'un traitement sur l'autre, avec Python (suivant le tableau 11.2 tiré de books.google.be/books, "Geo-information: Technologies, Applications and the Environment", Lemmens, M., 2011, Springer). La régression sera d’autant meilleure que le RMSE est petit.

import numpy as np
# première série de points
x1 = [194184.81,194286.47,194289.02,195292.21,196502.49]
x2 = [194186.12,194283.64,194288.34,195294.12,196501.84]
# deuxième série de points 
y1 = [469054.43,469550.98,469945.65,470539.12,470941.38]
y2 = [469053.24,469549.89,469943.46,470542.21,470942.73]
# calcul de des erreurs types (RMSE) sur x et y
RMSEx = np.sqrt(np.sum([(x1[i] - x2[i])**2 for i in range(len(x1))])/float(len(x1)))
RMSEy = np.sqrt(np.sum([(y1[i] - y2[i])**2 for i in range(len(y1))])/float(len(y1)))
#calcul du RMSE planaire 
RMSEplanaire = np.sqrt((a1*a1)+(b1*b1))
 
# résultat avec 3 chiffres significatifs
print("%.2f" % RMSEplanaire)
2.57

Le problème de ce genre de méthode est que toutes les incertitudes sont résumées en une seule valeur qui ne tient pas compte des variations de leurs distributions.

Définition d'un modèle pour les erreurs

Une erreur est estimée par un coefficient d'incertitude et qui dit incertitude pense à probabilité, mais il est cependant important de distinguer ici l'incertitude de variabilité d'une mesure due au caractère aléatoire de l’information (cas de la surface, par exemple) de celle due au caractère imprécis, vague d'une observation (connaissance limitée, incomplète, voire imprécise ou ignorance partielle), nommée incertitude épistémique (sans parler de l'incertitude liée aux calculs, aux traitements).  Supposons, par exemple, qu'une variable n'est connue que par ses bornes maximale et minimale, une telle information n’exprime alors pas une variabilité de type aléatoire, mais de l’imprécision qu'il est impossible à « probabiliser » suivant les méthodes statistiques classiques. Cela n'implique pas qu'il soit impossible de la traiter rationnellement, c'est pourquoi diverses solutions existent.

Incertitude de variabilité (approche probabiliste)

Dans cette approche, pour pouvoir estimer une incertitude, il est  nécessaire d'utiliser un modèle mathématique et/ou statistique. Une incertitude est alors considérée comme une variable aléatoire limitée à une certaine plage (range) et/ou à une certaine distribution des valeurs possibles. Elle peut être décrite statistiquement par une fonction de distribution des probabilités (Probability Distribution function, pdf). Par exemple :

distribution de probabilité binormale de la position d'un point xy

En utilisant ces hypothèses, il est possible d'émettre des jugements sur la précision d'un objet spatial ou d'un attribut (par des moyennes, des variances, des covariances, des écarts-types ou intervalles de confiance). Mais, dans le domaine spatial, il est aussi nécessaire de spécifier le degré de corrélation spatiale et de corrélation simple, surtout dans l'analyse des attributs. Les causes de la corrélation spatiale (vraies, trompeuses, induites par un traitement ou par une relation causale entre des localisations proches) sont décrites dans les ouvrages cités. Il y a de nombreuses méthodes pour calculer les degrés de corrélations spatiales (indice de Moran, etc.) ou de corrélations simples, mais ce n'est pas le but de l'article. Il est cependant important de noter que ces corrélations peuvent avoir une influence certaine dans la propagation des incertitudes.

Incertitude épistémique 

Plutôt que de partir des valeurs puis calculer les incertitudes, les approches suivantes changent de paradigme : le raisonnement se fait dès le départ sous la contrainte de l'incertitude. Parmi celles-ci :

- le calcul d'intervalle flou, ensemble flou, logique floue  (fuzzy set theory)

Par nature, le flou se réfère à l'imprécision et à l'incertitude. La théorie des ensembles flous et la logique floue se basent sur la prise en compte d'ensembles définis de façon imprécise. À l'inverse de la logique booléenne, la logique floue permet à une condition d'être en un autre état que vrai ou faux (voir fr.wikipedia.org/wiki/Ensemble_flou,  fr.wikipedia.org/wiki/Logique_floue ou franck-dernoncourt.developpez.com/tutoriels/algo/introduction-logique-floue/). Cette condition est exprimée sur une échelle quantitative :

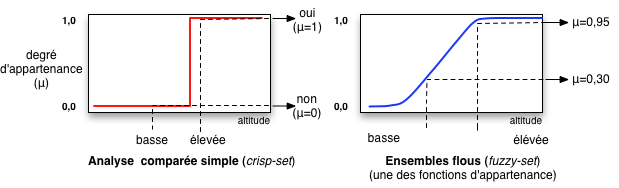
De la même manière qu’une distribution de probabilité permet de représenter une information relative à une variabilité aléatoire, une distribution de possibilité permet de représenter une information qui est incomplète ou imprécise. Le calcul est alors tout simplement un calcul d’intervalle classique, mais effectué sur des intervalles pris à différents degrés de vraisemblance. Le résultat est un intervalle de possibilité.

- l'incertitude bayésienne, probabilités conditionnelles, inférence bayésienne

L'approche bayésienne se différencie des autres méthodes, car elle permet au chercheur d'utiliser des jugements à priori exprimant des connaissances (de tous les facteurs du problème) et des degrés de confiance. En simplifiant outrageusement, elle permet donc de mettre à jour une distribution à priori concernant la quantité incertaine, en utilisant un modèle (exprimant la vraisemblance des données observées) pour obtenir une distribution à posteriori. La probabilité d'un événement est définie comme le degré de croyance (degree of belief) quant à la survenue de cet événement.
La démarche est la suivante:

- définition d'une distribution de probabilité a priori qui ne tient pas compte des résultats de l’étude;
- mise à jour de la vraisemblance du modèle paramétrique admis pour la population de référence, au  regard des données issues des observations;
- combinaison des deux sources pour produire une synthèse globale sous forme de distribution de probabilité a posteriori;
- les ajustements nécessaires sont calculés en utilisant le théorème de Bayes.

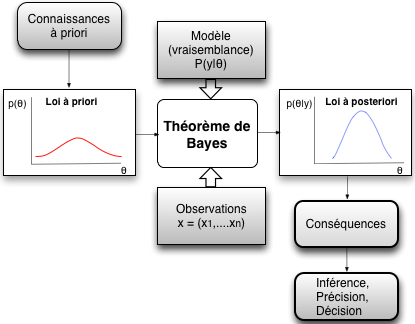
schéma adapté de "Éveiller la curiosité de l'étudiant pour la statistique bayésienne via un problème décisionnel fondé sur une tragédie réelle", Boreux, J.-J., Parent, E., Bernier, J., 2010, disponible à cfies2010.ulb.ac.be/files/Presentations/Presentation_Boreux.pdf

Avec cette technique, il est alors possible de distinguer pour un paramètre une « fourchette », appelée habituellement intervalle de crédibilité ("Et si vous étiez un bayésien qui s’ignore ?", Lecoutre, B., 2005, disponible à www.rocq.inria.fr/axis/modulad/archives/numero-32/lecoutre-32/lecoutre-32.pdf).   

- les fonctions de croyance (théorie de Dempster-Shafer)

Elles permettent d'assigner des masses de probabilité aux valeurs (fr.wikipedia.org/wiki/Th%C3%A9orie_Dempster-Shafer). Elles fournissent un mode de représentation de l’information qui s’applique à la fois au problème de la variabilité et au problème de l’imprécision ou ignorance partielle. Elles permettent de calculer un intervalle de croyance (voir par exemple, "Projet IREA – Traitement des incertitudes en évaluation des risques d’exposition" , www.brgm.fr/Rappor)

Ce sont diverses facettes qu’il convient de distinguer pour un traitement cohérent de l’incertitude, mais nous nous limiterons ici à l'approche probabiliste.

Principe de l'analyse de la propagation des incertitudes dans le domaine géospatial (suivant Heuvelink, incertitude de variabilité)

Le problème peut être formalisé mathématiquement de la manière suivante : si U est le résultat d'une opération g dans un SIG sur les n attributs de Ai  ou sur n variables A (voir les articles de Heuvelink) :

L'objectif est de déterminer l'incertitude sur le résultat U en fonction des incertitudes des n données de départ suivant le traitement g.

Exemples de traitements suivant cette formulation :

angle de pente = g(MNT)
changement de projection = g(coordonnées de départ)
surface d'un rectangle = g(longueur, largeur)
acidification d'un sol = g(diverses propriétés du sol)
etc.

Dans le cas ou g est une fonction linéaire, le calcul est relativement facile (la moyenne et la variance de U peuvent être directement dérivées), dans les autres cas, non. Dans le cas où les variables de départ sont des variables numériques, il est possible d'utiliser les techniques de calcul des propagations d'incertitudes des métrologues.

Techniques de traitement des incertitudes dans le domaine géospatial

Différentes méthodes, les unes plus complexes que d’autres, certaines probabilistes, d'autres non, existent pour déterminer cette incertitude. Nous nous limiterons ici au calcul de la propagation des incertitudes numériques lors des calculs divers, dans l'approche probabiliste (incertitude = variabilité). Il y a lieu de distinguer deux approches :

- analyse de sensibilité (sensitivity analysis)

Le principe est d'analyser comment un modèle (numérique et/ou conceptuel) est sensible aux variations des données d’entrée (le but est d'identifier les parties du modèle qui sont critiques et celles qui ne le sont pas). Cette technique est utilisée, par exemple, dans l'interpolation des MNT. Bien que son objectif n'est pas de quantifier l'incertitude résultante, ses résultats pourraient être utilisés dans ce contexte mais ce n'est pas du calcul d'incertitudes. Il existe de nombreuses solutions pour créer un MNT, mais l'analyse ne permet pas de décider de manière non ambigüe quelle est la « meilleure » d'entre elles. Elle est disponible dans des logiciels SIG comme ArcGIS ou GRASS GIS dans le cas de rasters.

- analyse de propagation des incertitudes

Le but est d'analyser comment les incertitudes liées aux données d’entrée se propagent dans le modèle résultant.

Dans le cas des incertitudes de variabilité, les deux techniques habituellement utilisées sont :

- techniques de simulation du résultat (Monte Carlo, simulation géostatistique)

- techniques d'ajustement (approximation linéaire, de Taylor)

Leur principe est de « rester dans le monde Gaussien », c’est à dire dans un modèle où on manipule des lois de Gauss. Elles seront illustrées par la suite à l'aide de Python.

Dans le cas des incertitudes épistémiques, il existe diverses approches qui ne seront que citées ici avec leur utilisation dans les logiciels SIG :

- utilisant les ensembles flous, logique floue  (fuzzy set theory)

Depuis les années 1980, des applications de la logique floue ont été développées avec succès dans des domaines très variés ("Modeling Uncertainty with Fuzzy Logic, With Recent Theory and Applications", Celikyilmaz, A., Türksen, I.B., 2009, Springer, www.amazon.com/Modeling-Uncertainty-Fuzzy-Logic-Applications/dp/3540899235#reader_3540899235), notamment en géologie (voir "Fuzzy Logic in Geology" Demicco, R.V. & Klir, G.J., éditeurs, 2004, Elsevier, www.amazon.com/Fuzzy-Logic-Geology-Robert-Demicco/dp/0124151469). Dans le domaine géospatial, un exemple courant est le problème des limites liées aux processus de classification. En géologie, par exemple, les limites entre les diverses unités cartographiées (lithostratigraphie) ne sont pas précisément connues (elles sont floues), hormis dans des cas particuliers (le « Golden Spike » dans le cas de coupes géologiques continues, voir en.wikipedia.org/wiki/Global_Boundary_Stratotype_Section_and_Point, par exemple).

Ces applications existent dans le monde des logiciels SIG. Le pionnier a été IDRISI puis GRASS GIS avec les modules r.fuzzy, r.fuzzy.logic et r.fuzzy.system, Elles sont aussi disponibles dans SAGA GIS,  dans ArcGIS, surtout depuis la version 10, avec l'extension Spatial Analyst (help.arcgis.com/en/arcgisdesktop/10.0/help/index.html#//009z000000rn000000.htm et help.arcgis.com/en/arcgisdesktop/10.0/help/index.html#//009z000000rp000000.htm ), sans parler de R-Spatial, bien entendu. Un exemple démonstratif est donné dans "Fuzzy logic: Identifying areas for mineral development", Vickers, M. & Fleming, G., 2009, disponible à www.eepublishers.co.za/images/upload/PositionIT%202009/page%2036-40.pdf, avec l'extension Arc-SDM (Spatial Data Modeller) pour ArcGIS.

- utilisant les probabilités bayésiennes, réseaux bayésiens (Bayesian Networks, Bayesian Belief Networks)

Sous ce nom existe toute une gamme de techniques différentes utilisant les probabilités bayésiennes (réseaux bayésiens, réseaux de Markov, etc., voir fr.wikipedia.org/wiki/R%C3%A9seau_bay%C3%A9sien ou "Les Réseaux Bayésiens, Introduction Intuitive", Denis, J.B., 2007, disponible à w3.jouy.inra.fr/unites/miaj/public/matrisq/Contacts/abari.07_03_12.expo2.pdf) par exemple). Elles permettent, entre autres choses, de calculer la probabilité des données non observées en fonction des informations observées. Cette approche de la propagation des incertitudes est particulièrement utile lorsqu'il y a des informations insuffisantes pour le processus décisionnel scientifique en raison de la rareté des données et la complexité.

A titre d'exemple, le système Windows de Microsoft utilise cette approche bayésienne pour diagnostiquer les problèmes rencontrés depuis Windows 98.

Elle est aussi parfaitement adaptée à la modélisation SIG (voir par exemple "Error Models in Geographic Information Systems Vector Data Using Bayesian Methods" disponible à www.web-e.stat.vt.edu/dept/web-e/tech_reports/TechReport07-1.pdf). Il y a de nombreuses références à ce sujet sur Internet (dont celle d'ESRI, www.esri.com/news/arcuser/1009/beliefnetworks.html) en particulier pour l'étude des répartitions spatiales des objets ou l'analyse des risques.

Cette technique est implémentée dans R-Spatial, IDRISI et partiellement, dans GRASS GIS (r.infer), SAGA GIS, et dans des scripts de ArcGis, surtout pour traiter les rasters.

- utilisant le modèle de Dempster-Shafer (belief modelling, Dempster-Shafer Theory of Evidence)

Ces techniques ont été utilisées dès 1999 dans le monde géospatial (voir par exemple "Belief modeling with Arcview GIS",  proceedings.esri.com/library/userconf/proc99/proceed/papers/pap295/p295.htm ) surtout dans la modélisation des risques (incertitude de la règle de décision, Decision Rule Uncertainty, etc., voir "Aide à la décision et SIG", disponible à www.ipt.univ-paris8.fr/vgodard/enseigne/master1/memomas/mem11mas.htm   ou www.forumsig.org/showpost.php) 

Elle est implémentée, encore une fois, dans IDRISI , dans certains modules ou scripts pour ArcGIS et dans  R-Spatial.

Techniques de propagation des incertitudes de variabilité numérique (avec Python)

Simulation du résultat (Monte-Carlo, simulation géostatistique)

La simulation de Monte-Carlo est une méthode probabiliste qui vise à générer des résultats simulés à partir d'une distribution d'une probabilité spécifiée qui décrit statistiquement les données d'entrée (fr.wikipedia.org/wiki/M%C3%A9thode_de_Monte-Carlo). Cette méthode est, en pratique, réalisée par de multiples exécutions de la fonction g  en faisant varier aléatoirement les variables d'entrée suivant une distribution statistique. Il faut donc en assigner une à chaque variable d'entrée, générer N fois la fonction g, puis analyser le résultat de l'opération finale. C'est donc une simulation pure du résultat qui remplace la notion d’erreur accidentelle par celle d’incertitude aléatoire.

Cette opération est illustrée par le calcul de la surface d'un carré de 100 m x 100 m avec une incertitude binormale de rayon de 2 m sur les coordonnées des sommets. Un exemple en ligne, réalisé par une applet Java,  est disponible sur le site www.ncgia.ucsb.edu/~ashton/demos/areasim/area.html

Il est possible de le faire en Python, en considérant, comme dans l'application citée, que l'incertitude suit une loi gaussienne, avec le module random (random.gauss) ou avec le module Numpy (numpy.random.normal).

Les surfaces sont générées N fois, comme dans l'exemple cité précédemment:

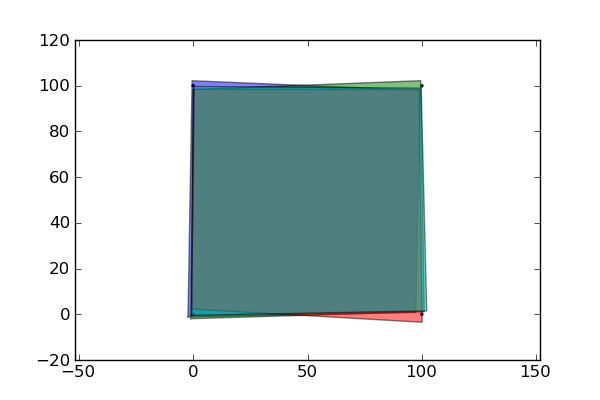
figure réalisée avec le module Python matplotlib

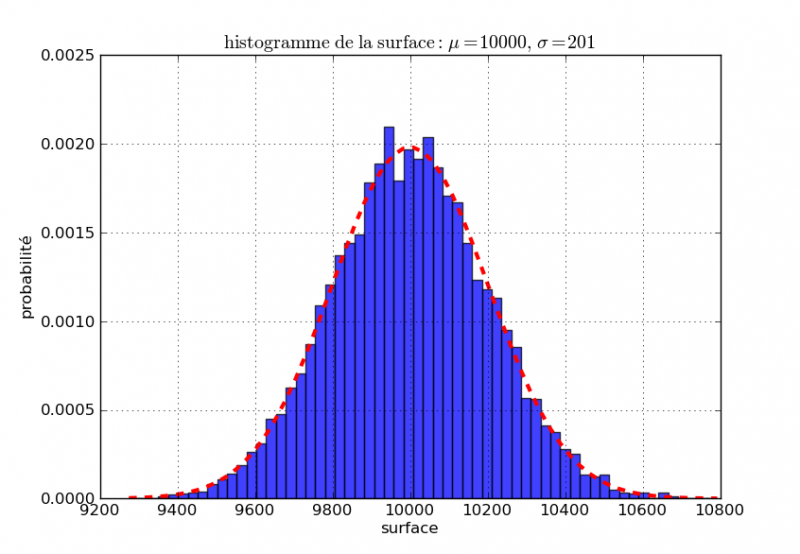
Au bout de N itérations, la moyenne et la déviation standard sont calculées et un histogramme des valeurs de surface obtenues peut être figuré à l'aide du module matplotlib.

première solution

La première solution consiste à calculer une largeur et un longueur à partir des coordonnées des points suivant la loi de probabilité gaussienne puis de calculer N fois une surface résultante :

import matplotlib.mlab as mlab
from random import *
from math import *
import pylab
# coordonnées de 2 sommets puisque longueur = largeur
x1 = 0
x2 = 100
y1 = 0
y2 = 100
stv = 2 # déviation standard pour le rayon
# une déviation standard de 2 m en rayon sur chaque coin correspond à une déviation standard en x ou y de stv/sqrt(2)
stv = stv/sqrt(2)
 
surfaces = []
# nombre d'itérations
N = 10000
 
#calcul des surfaces avec random.gauss
for n in range(N):
        longueur = gauss(sqrt((x2-x1)**2 + (y1-y1)**2),stv) 
        largeur = gauss(sqrt((x1-x1)**2 + (y2-y1)**2),stv)
        surf = longueur*largeur
        surfaces=surf+[surface]
 
mu = pylab.mean(surfaces)
sigma = pylab.std(surfaces)
# résultats bruts d'une des simulations
print mu, sigma
9999.95247682 201.33026996
# résultats en tenant compte de la rêgle des chiffres significatifs
print "Resultats :"
print "Moyenne = ","%.f" % mu
print "déviation standard  = ", "%.f" % sigma
 
Resultats :
Moyenne =  10000
déviation standard  =  201
 
# tracé de l'histogramme
n, bins, patches = pylab.hist(surf, 60, normed=1, facecolor='blue', alpha=0.75)
y = mlab.normpdf( bins, mu, sigma)
l = pylab.plot(bins, y, 'r--', linewidth=3)
#plt.xlabel('Smarts')
pylab.xlabel('surface')
pylab.ylabel(u'probabilité')
pylab.title(r'$\mathrm{histogramme\ de\ la\ surface:}\ \mu=%.f,\ \sigma=%f$' %(mu, sigma))
pylab.grid(True)
pylab.show()

Histogrammes pour les longueurs et les largeurs calculées par le script avec random.gauss :

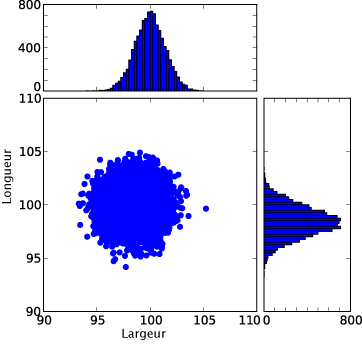
figure réalisée avec le module Python matplotlib

Histogramme final pour la surface :

figure réalisée avec le module Python matplotlib

Puisque c'est un carré, pourquoi  ne pas calculer la surface avec la simple formule :

longueur d'un côté x longueur d'un côté

Dans ce cas,  les variables ne sont pas indépendantes puisque ce sont les mêmes. De ce fait, il ne peut pas y avoir de compensation aléatoire des erreurs : si la longueur est, par exemple, surestimée,  l'excès le sera aussi. Dans le premier cas analysé, il peut arriver qu'une longueur soit sous-estimée et l'autre surestimée, mais il y a une possibilité de compensations avec les largeurs. (www.incertitudes.fr/Incertitudes.html)

for n in range(N):
        longueur = gauss(sqrt((x2-x1)**2 + (y1-y1)**2),stv) 
        surf = longueur**2 
        surfaces=surf+[surface]
 
Resultats :
Moyenne =  10000
déviation standard = 282

solution « correcte »

De plus, dans le cas présent où l'incertitude est celle des sommets, cette simulation n'est pas formellement « correcte » et il n'est pas possible de la faire en calculant séparément la longueur et la largeur. Une largeur et une longueur possèdent un sommet xy commun, elles sont donc corrélées. Le bon calcul impose donc de calculer de manière probabiliste les coordonnées des sommets (plutôt que celles des longueurs et des largeurs), puis la surface. De plus, pour être rigoureux, un quadrilatère ayant 4 côtés différents, la surface doit être calculée sur cette base (un grand merci à Éric Lebigot).

# calcul des surfaces 
for n in range(N):
    # évaluation de chaque sommet
    x1 = gauss(0, stv)
    y1 = gauss(0, stv)
    x2 = gauss(100, stv)
    y2 = gauss(0, stv)
    x3 = gauss(0, stv)
    y3 = gauss(100, stv)
    x4 = gauss(100, stv)
    y4 = gauss(100, stv)
    x1 = gauss(0, stv)
    y1 = gauss(0, stv)
    x2 = gauss(100, stv)
    y2 = gauss(0, stv)
    x3 = gauss(0, stv)
    y3 = gauss(100, stv)
    x4 = gauss(100, stv)
    y4 = gauss(100, stv)
    # calcul de surface adapté
    surface = sqrt((x2-x1)**2+(y2-y1)**2)*sqrt((x3-x1)**2+(y3-y1)**2)/2+sqrt((x4-x2)**2+(y4-y2)**2)*sqrt((x4-x3)**2+(y4-y3)**2)/2
    surf=surf+[surface]
 
mu = pylab.mean(surfaces)
sigma = pylab.std(surfaces)
# résultats bruts d'une des simulations
print mu, sigma
10003.1814816 200.382615819
# résultats en tenant compte de la rêgle des chiffres significatifs
print "Resultats :"
print "Moyenne = ","%.f" % mu
print "déviation standard  = ", "%.f" % sigma
 
Resultats :
Moyenne =  10003
déviation standard  =  200

Histogrammes pour les points xi,yi calculés par le script avec random.gauss :

..................

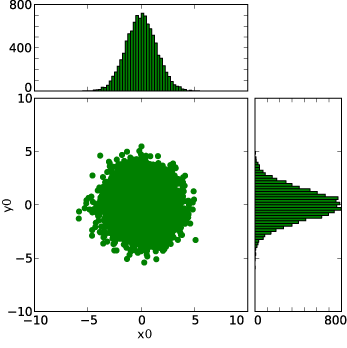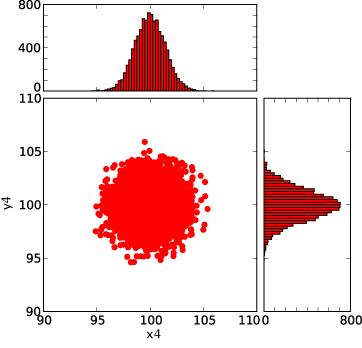
de x0,y0 à x4,y4, figures réalisées avec le module Python matplotlib

Dans ce cas particulier, il n'y a pas de grandes différences , mais cette dernière solution est valable pour tous les quadrilatères.  Elle permet aussi de formuler la simulation avec le module Numpy :

import numpy as np
 
x1 = np.random.normal(0, stv, N)
y1 = np.random.normal(0, stv, N)
x2 = np.random.normal(100,stv, N)
y2 = np.random.normal(0, stv, N)
x3 = np.random.normal(0, stv, N)
y3 = np.random.normal(100, stv, N)
x4 = np.random.normal(100, stv, N)
y4 = np.random.normal(100, stv, N)
 
# calcul des surfaces 
surfaces = np.sqrt((x2-x1)**2+(y2-y1)**2)*np.sqrt((x3-x1)**2+(y3-y1)**2)/2+np.sqrt((x4-x2)**2+(y4-y2)**2)*np.sqrt((x4-x3)**2+(y4-y3)**2)/2
 
# résultats d'une des simulations
print mu, sigma
9999.1573234 199.631782423
# résultats en tenant compte de la rêgle des chiffres significatifs
print "Resultats :"
print "Moyenne = ","%.f" % mu
print "déviation standard  = ", "%.f" % sigma
 
Resultats :
Moyenne =  10000
déviation standard =  200
 

conclusions

La démarche montre l'importance de l'indépendance des variables et des corrélations entre variables dans le cas des incertitudes.

Le résultat qui devrait être donné par un SIG est donc 10000 ± 200 mètres carrés et non 10000 mètres carrés ou 9999,1573234 mètres carrés.

Les résultats sont tous comparables avec ceux de l'applet Java. C'est une méthode qui peut être très coûteuse en temps de calcul, mais qui est à peu près impossible à battre en précision.  Elle est implémentée dans certains modules de GRASS GIS et dans certains scripts pour ArcGIS.

simulation alternative

Une variante est la simulation géostatistique élaborée à l'aide de techniques de prédiction spatiales telles que le krigeage (« fonctions de transfert »).  Le progiciel R avec ces librairies spatiales permet de le faire.

Ajustements, approximations linéaires, de Taylor

Le principe est d'approximer la fonction g par une fonction linéaire qui est, localement, une bonne approximation du résultat. C'est le véritable calcul d'incertitude, peu utilisé dans les logiciels SIG. C'est pourtant la principale méthode prônée dans les ouvrages cités et par le GUM.

Pour approcher cette notion de manière intuitive, considérons la courbe représentative d'une fonction. Quel que soit le point que l'on choisit sur la courbe, il est possible de tracer une tangente, c'est-à-dire une droite qui épouse localement la direction de cette courbe. Si l'on s'en approche en zoomant suffisamment, on aura de plus en plus de mal à distinguer la courbe de sa tangente. Pour cette raison la fonction linéaire dont le graphe est la ligne tangente de y = f(x) à un point précis a, f(a) est appelée approximation linéaire de f(x) au point x = a.

Si l'on se rappelle que la pente de cette droite tangente est le nombre dérivé de la fonction f en x=a, noté f'(a), cette droite est facile à retrouver :

Appliquons à un carré dont la U = surface = g( longueur d'un côté x longueur d'un côté) avec le module Scipy (un des modules permettant de calculer facilement les dérivées) :

from  scipy.misc import *
 
# fonction g de la surface d'un carré
def surface(x):
   return x * x
 
# dérivée de la fonction surface au point x = 2 -> 
# pente de la tangente à la courbe surface(x) en ce point noté g'(x)
print derivative(surface,2) 
4.0
 
# pour un longueur de x = 2, calcul de la surface : surface(x) noté g(x)
print surface(2)
4.0

La courbe de la fonction surface passe donc par le point (2,4) qui est commun à la tangente qui passe par ce point et dont la pente est maintenant connue. Il suffit alors d'appliquer l'équation :

y−y1 = pente * (x−x1) = g'( 2) * (x - x1)
y − 4 =  4 * (x − 2)
y − 4 =  4x − 8
y = 4x − 4

qui est l'équation de l'approximation linéaire de la fonction g au point 2,4, notée ici

g(a) = g'(a)(x-a)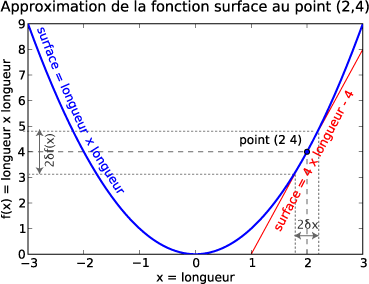

figure réalisée avec le module Python matplotlib

En analyse, le théorème de Taylor montre qu'une fonction plusieurs fois dérivable au voisinage d'un point peut être approximée par une fonction polynôme dont les coefficients dépendent uniquement des dérivées de la fonction en ce point. La méthode permet donc de calculer des approximations de plusieurs ordres qui s'approchent peu à peu de la courbe réelle (voir simulations mathématiques à www.mathdemos.org/mathdemos/TaylorPolynomials/)

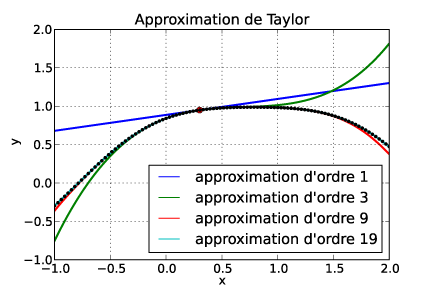
figure réalisée avec le module Python matplotlib

L'approximation de Taylor d'ordre 1 est équivalente à l'approximation linéaire de la fonction.

Ce modèle d'approximation, appelé approximation linéaire de Taylor, peut être résumé, dans le cas des SIGs, par la figure suivante (adaptée de la figure "Taylor series method, one-dimensional case" dans Heuvelink, G.B.M dans "WORKSHOP Spatial Uncertainty Propagation", 2008,  www.spatial-accuracy.org/sites/default/files/Lecture2_SUP.pdf)

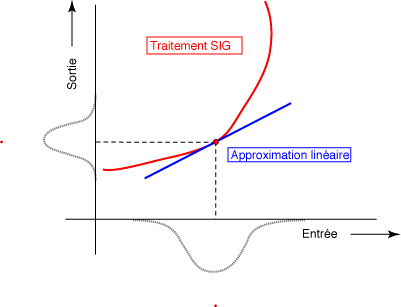
C'est aussi une des approches classiques du GUM (voir  "Sur les incertitudes de mesure", André R., 2008, disponible à  www.math.u-bordeaux1.fr/ecaq/cours_pdf/EcAq2008_20_R.Andre.pdf)

1. Modèle inversible;
2. Incertitudes = variances des paramètres;
3. Propagation des variances dans un modèle « linéarisé »;
4. Variance → incertitude élargie, intervalle de confiance.

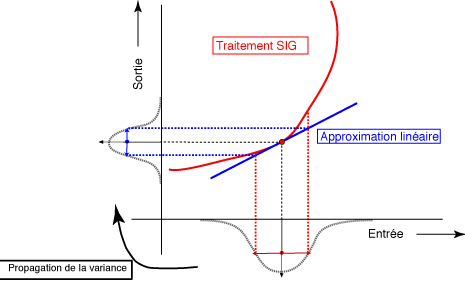
Malgré le caractère relativement complexe de la définition, il y a beaucoup moins de problèmes avec Python, car Éric Lebigot a créé le magnifique module Python uncertainties qui permet de faire tous ces calculs. (il y a aussi un autre module Python, upy, beaucoup moins intuitif à utiliser, et une solution en JavaScript: "Propagazione degli errori in dati geografici" à www.malg.eu/propagazione_errori.php).

La méthode utilisée par le module uncertainties consiste à calculer une série de Taylor d'ordre 1 de toutes les fonctions. Les relations sont supposées être linéaires. Il permet donc le calcul des déviations standards des expressions mathématiques par l'approximation linéaire.

Reprenons l'exemple de la surface d'un carré illustré avec la simulation de Monte-Carlo. A titre de comparaison, nous choisissons la même déviation standard que celle utilisée dans le cas de la simulation de Monte-Carlo, mais le cas est différent puisque c'est une incertitude qui porte cette fois-ci sur la longueur d'un côté (et pas sur les sommets) :

from uncertainties import ufloat
# à titre de comparaison, la valeur de la déviation standard  stv est la même 
# que celle utilisée dans la simulation de Monte Carlo
 
from uncertainties.umath import *  
# ce sous-module permet de capturer les fonctions du module math, 
# ce qui permet d'utiliser les fonctions cos(), sin(),etc. avec des incertitudes.
 
# fonction g de la surface
def surface(x,y):
   return x * y
 
longueur = ufloat((100,stv)) # 100 ± stv
largeur  = ufloat((100,stv)) # 100 ± stv
 
print surface(longueur,largeur)
10000.0+/-200.0
# détail, moyenne, déviation standard
print surface.nominal_value
10000.0
print surface.std_dev()
200.0
# résultats en tenant compte de la rêgle des chiffres significatifs
résultat = surface(longueur,largeur)
print "%.f" % résultat.nominal_value,"+/-","%.f" % résultat.std_dev()
10000+/-200

Le module tient aussi compte de l'indépendance et de la corrélation des variables. Que se passe-t-il si on utilise la simple fonction longueur x longueur (puisque c'est un carré) :

def surface(x):
   return x * x
 
longueur = ufloat((100,stv))
print surface(longueur)
10000.0+/-282.842712475
# résultats en tenant compte de la rêgle des chiffres significatifs
print "%.f" % surface.nominal_value,"+/-","%.f" % surface.std_dev()
10000+/-283

Ce problème d'indépendance des variables est illustré d'une autre manière par www.incertitudes.fr/Incertitudes.html dans le calcul des distances :

« un voyageur de commerce part de Paris, va à Lyon, puis à Nice et revient pour finir à Lyon. Celui-ci indique que la distance Paris-Lyon est de 465 km et la distance Lyon-Nice de 479 km. Les distances sont estimées à 10 km près. Déterminez la distance Paris-Nice puis celle de l'aller-retour Lyon-Nice »

from uncertainties import ufloat
from uncertainties.umath import *
Paris_Lyon = ufloat((465,10))
Lyon_Nice = ufloat((479,10))
Paris_Nice = Paris_Lyon + Lyon_Nice
print Paris_Nice
944.0+/-14.142135623730951
# résultats en tenant compte de la rêgle des chiffres significatifs
print "%.f" % Pa_Nic.nominal_value,"+/-","%.f" % Pa_Nic.std_dev()
944 +/- 14
 
Lyon_Nice_Lyon = Lyon_Nice * 2
print Lyon_Nice_Lyon
958.0+/-20.0
print "%.f" % Ly_Nic_Ly.nominal_value,"+/-","%.f" % Ly_Nic_Ly.std_dev()
958 +/- 20
 
# si les 2 variables n'étaient pas corrélées (indépendantes)
x = ufloat((479,10))
y = ufloat((479,10))
test = x + y
print "%.f" % test.nominal_value,"+/-","%.f" % test.std_dev()
958 +/- 14

Dans le cas de l'aller-retour Lyon-Nice, les variables ne sont pas indépendantes.

Toutes les possibilités du module sont détaillées à packages.python.org/uncertainties/index.html

Les corrélations entre les variables sont aussi automatiquement traitées par le module, quel que soit le nombre de variables impliquées alors qu'il doit être spécifié dans www.malg.eu/propagazione_errori.php

Le problème de l'aire, tel qu'il est figuré dans la simulation de Monte-Carlo (en fonction des 4 sommets), n'est pas adapté à la méthode de propagation d'erreur linéaire, car il faut que les fonctions manipulées aient de bonnes approximations linéaires sur les intervalles d'erreur, ce qui n'est pas le cas dans l'exemple proposé. Éric Lebigot, en attendant qu'il ajoute à uncertainties la possibilité de faire les calculs à des ordres plus élevés, m'a fourni une solution qui marche, mais je ne vais pas continuer à vous « noyer » dans les codes Python...

Conclusions

Tout ce que j'espère est de vous avoir donné une idée de l'importance du rôle des incertitudes et du calcul des incertitudes dans les traitements effectués par un logiciel SIG, malgré la relative complexité du thème.

Aucun traitement n'améliorera jamais l'incertitude présente dans les données de départ, tout au contraire. Or un logiciel donnera toujours une impression de précision fallacieuse dans les résultats qu'il va fournir, toujours plus précis que les variables de départ (voir "What Every Computer Scientist Should Know About Floating-Point Arithmetic " à  docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html, un lien parmi d'autres). Le traitement lui-même va donc apporter sont lot d'incertitudes. Ainsi, si on travaille sur des données fournies au mètre près, vous comprendrez, j'espère, qu'il est faux de fournir des résultats en mètres avec des décimales, après traitements divers (erreur encore trop souvent rencontrée...).

Dans le monde des logiciels SIG, cet aspect n'est, malheureusement, pas encore assez pris en compte et le thème reste encore trop confiné dans le monde de la recherche scientifique. Le lien entre ce domaine et la métrologie reste aussi trop ténu chez les utilisateurs. Cela commence à venir, comme illustré dans mon propos, avec les logiciels cités dans chaque approche, mais ce n'est pas facile. Pourtant, une première solution, simple, serait déjà de respecter la règle des chiffres significatifs...

Il existe des logiciels spécialisés pour traiter ce problème comme DUE (« Data Uncertainty Engine »), disponible gratuitement sur le site www.spatial-accuracy.org/workshopSUP et adapté au domaine géospatial ou ceux disponibles pour la métrologie (en.wikipedia.org/wiki/List_of_uncertainty_propagation_software), mais je trouve que le module Python uncertainties est plus simple à utiliser directement et pourrait être utilisé dans tous les logiciels SIG qui utilisent Python (comme ArcGIS, Quantum GIS, GRASS GIS ou GvSIG) dans le cas des incertitudes de variabilité.

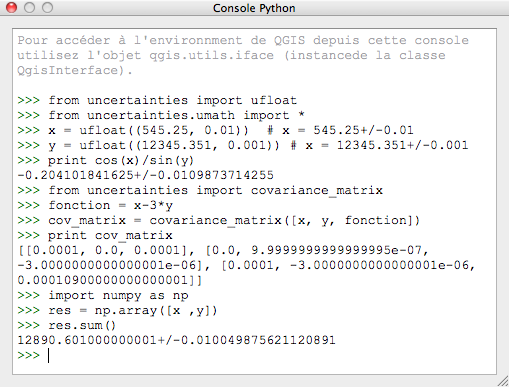
module uncertainties dans Qgis

« C'est l'incertitude qui nous charme. Tout devient merveilleux dans la brume »

Oscar Wilde, dans « Le portrait de Dorian Gray »

Tous les traitements ont été effectués sur Mac OS X avec Python 2.6.1, les modules matplotlib, SciPy, NumPy et uncertainties (version 1.8), Inkscape pour certaines figures et Gotlib, pour l'idée des engrenages ( freakonometrics.blog.free.fr/index.php, algoric.pagesperso-orange.fr/Priodik/dess1/mecaniq.htm)

licence Creative Commons Paternité-Pas d'Utilisation Commerciale-Partage des Conditions Initiales à l'Identique Commerciale 2.0 France