![]()
Parmi les normes de l'Open Geospatial Consortium, ou OGC figure Simple Features. Celle-ci définit le modèle géométrique à utiliser pour les entités vectorielles SIG ( Simple Feature Access - Part 1: Common Architecture: www.opengeospatial.org/standards/sfa, Simple Feature Access - Part 2: SQL Option: www.opengeospatial.org/standards/sfs) sous la forme de:
- un modèle de géométrie 2D pour les objets vectoriels (points, lignes, polygones...);
- le traitement des projections avec des identifiants de systèmes de référence spatiale ou SRID;
- un format de données "well-known" (WKT, WKB) pour le stockage de ces objets;
- les opérations spatiales (intersections, buffers, etc.) ;
- un schéma de base de données spatiale et un modèle d'accès.
Quelques exemples de représentation de géométries OGC au format WKT (sans SRID):
POINT (180 270)
LINESTRING (250 370, 180 330, 180 190)
POLYGON ((180 370, 130 310, 160 230, 160 230, 250 260, 180 370))
LINEARRING (180 370, 130 310, 160 230, 160 230, 250 260, 180 370)
Il est aussi nécessaire de bien comprendre les concepts d'intérieur, de limite et d'extérieur d'un objet géométrique, ainsi que sa dimension:
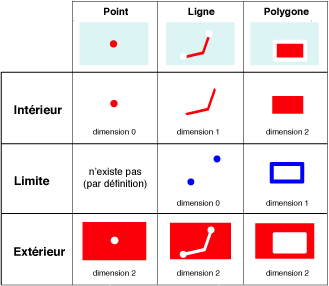
- l'intérieur d'une géométrie se compose de toute la géométrie à l'exception des limites
- la limite d'une géométrie est une géométrie de dimension inférieure
- l'extérieur d'une géométrie se compose de tous les points qui ne sont ni dans l'intérieur ni dans la limite;
Vu la composition de l’OGC (ESRI, Oracle et al.), cette norme devrait, en théorie, être respectée par tous les grands acteurs du SIG, mais ce n'est pas toujours le cas, comme toujours... (voir benjamin.chartier.free.fr/pro/). Dans le monde du libre, par contre, c'est le modèle utilisé, entre autres, par PostGIS qui se base sur la librairie GEOS, un élément de la Java Topology Suite (JTS).
En Java, il est possible d'utiliser cette Java Topology Suite seule grâce au programme JTS Test Builder (voir www.perrygeo.net/wordpress/ ) qui permet d'« explorer » les géométries OGC et les opérations spatiales.
En Python, Sean Gillies a créé le module Shapely pour permettre d'effectuer, en simplifiant, tout ce qu'il est possible de faire avec PostGIS, sans utiliser SQL ni Java, au niveau des géométries. Il est aussi basé sur la librairie GEOS, qui doit être installée auparavant (pour Windows, des distributions complètes de Shapely sont disponibles). Le module ne traite que les géométries dans un plan cartésien xy, sans projection (SRID). Sean Gillies part du principe qu'il vaut mieux travailler en coordonnées cartésiennes et une fois les démarches effectuées, les projeter ou les reprojeter avec d'autres outils. Je développerai dans la suite les points suivants:
- Les objets géométriques (points, lignes, polygones, multipoints, multilignes, multipolygones, multigéométriques);
- Les "constructeurs" ou comment créer des nouvelles géométries à partir d'un objet géométrique existant (buffer...);
- Les requêtes spatiales binaires (True, False) et les prédicats;
- les requêtes spatiales D9-IM de l'OGC (matrice de Clementini);
- L'analyse spatiale ou comment créer de nouveaux objets à partir de deux objets géométriques existants (union, intersection...) avec application à la matrice de Clementini;
- Les applications pratiques (shapefiles, PostGIS, projections, autre traitement mathématique)
- Comment dessiner les géométries avec Matplotlib et ma classe Plot_Shapely;
- Conclusions
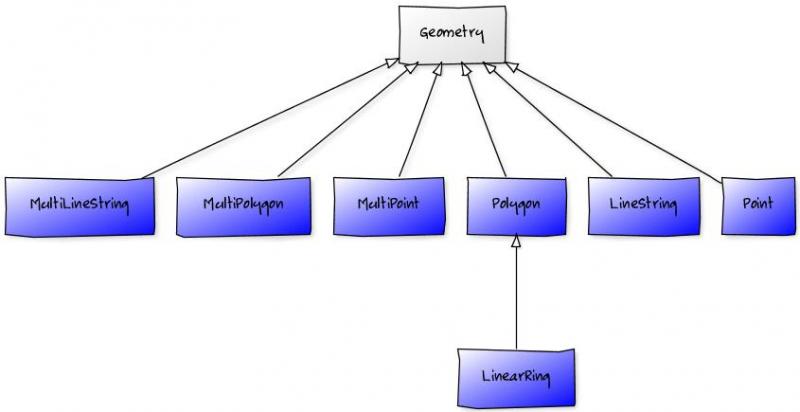
Les objets géométriques (points, lignes, polygones, multipoints, multilignes, multipolygones, multigéométriques)
Les principaux objets géométriques (classes) disponibles dans Shapely sont illustrés par le diagramme suivant créé avec Yuml (yuml.me/edit/25878f1a ):
La création d'un objet géométrique se fait en important sa classe géométrie:
from shapely.geometry import ...
- 4707 lectures
Shapely permet de visualiser l'objet au format WKT ou d'importer un objet défini en WKT. C'est cette forme qui sera utilisée dans la suite pour faciliter la compréhension.
wkt
- 4821 lectures
Toutes les figures ont été faites avec le module matplotlib. Nous détaillerons la démarche par la suite.


Un point est construit à partir de ses coordonnées xy (z). Son aire est par définition nulle. L'objet MultiPoints est une collection de points
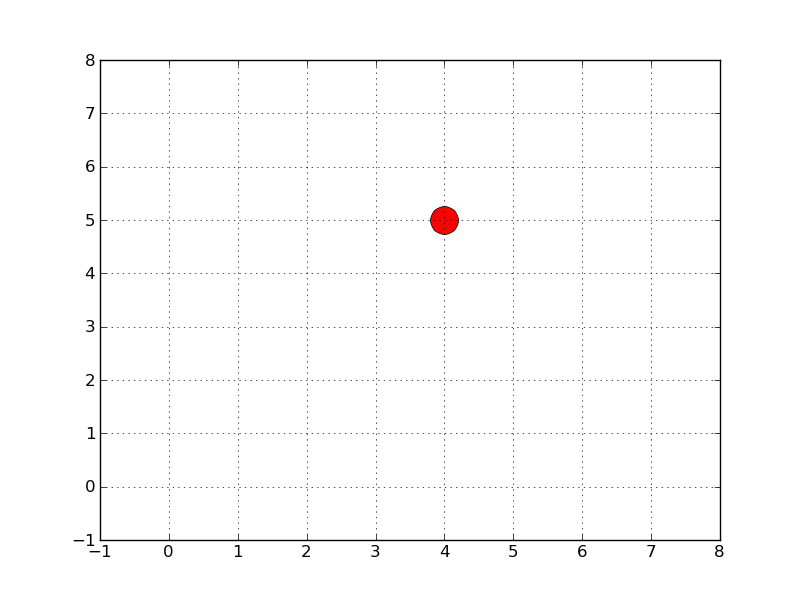
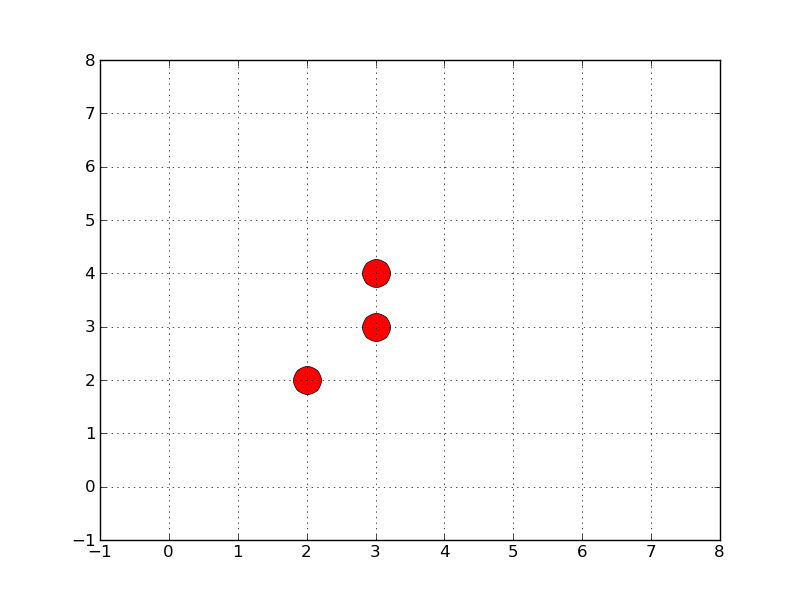
points - multipoint
- 4954 lectures


Un LineString est une ligne, définie par l'OGC comme une séquence ordonnée de deux à plusieurs Points. Un MultiLineString est une collection de lignes (LineString)
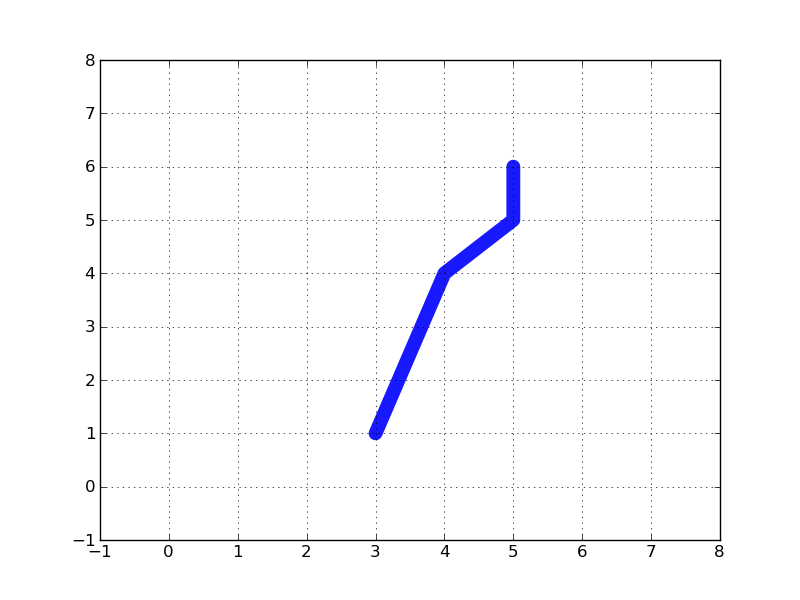
lignes - multilignes
- 5149 lectures
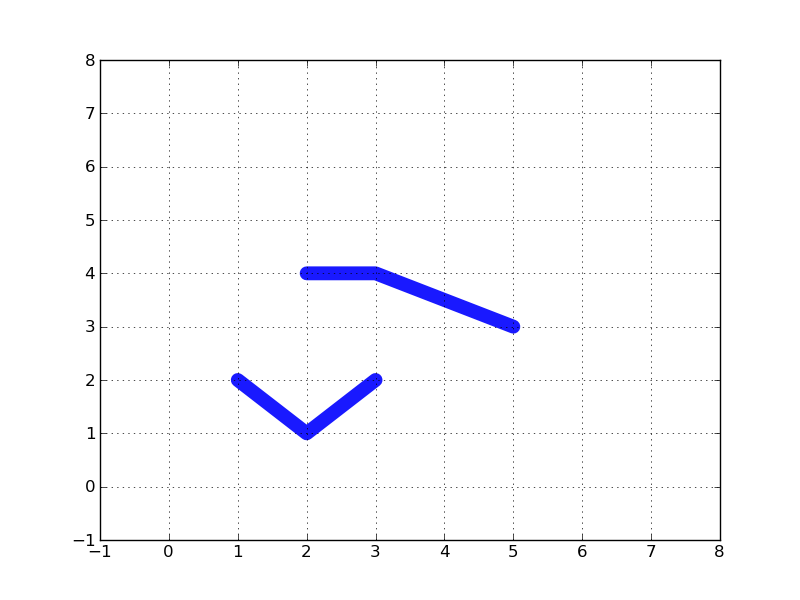
traitement lignes
- 3855 lectures


Un polygone s.s. peut être défini comme une aire simple ou en « anneau » (« troué »). Il est défini par une ou des séquences ordonnées de points.
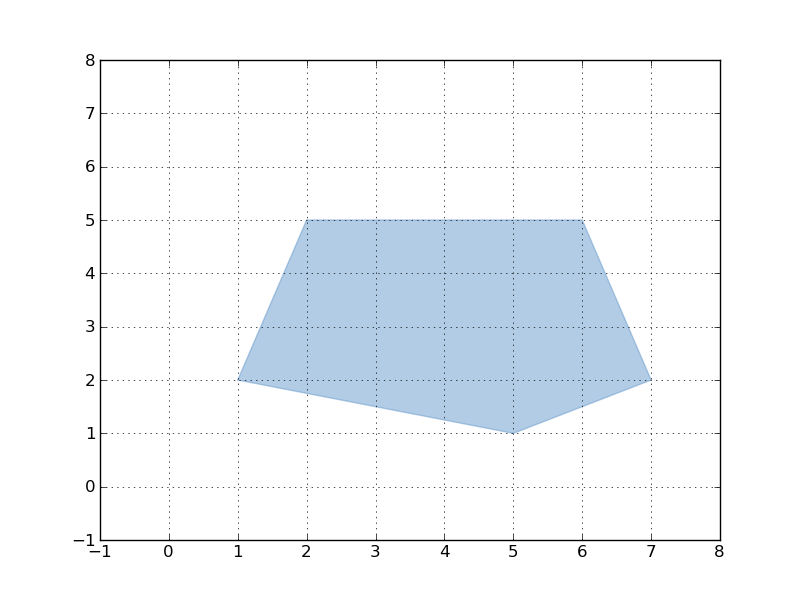
polygones
- 3597 lectures

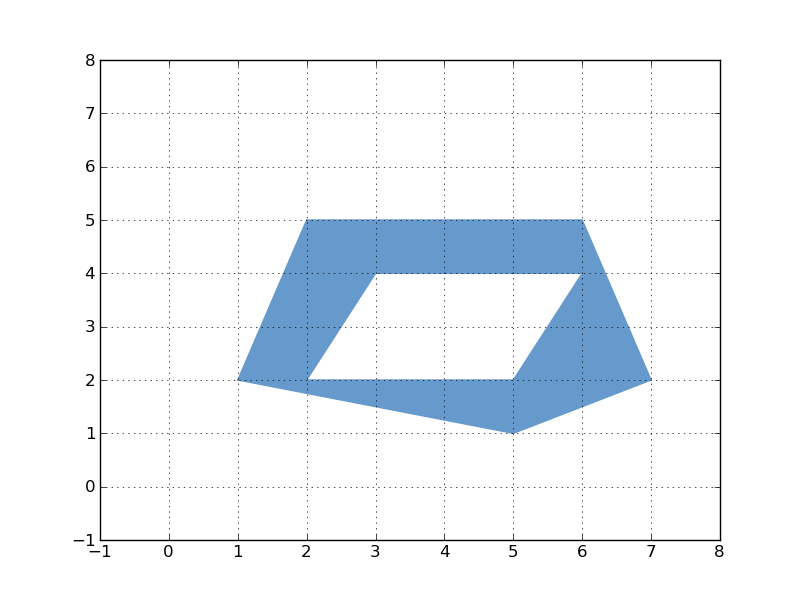
Les limites extérieures et intérieures d'un polygone sont des lignes fermées. C'est pourquoi le concept de LinearRing a été introduit par l'OGC pour les différencier des LineString. Dans Shapely, Sean Gillies en fait bien une sous-classe de Polygon.
linearring - polygone
- 3693 lectures
C'est à partir de ces LinearRing que les coordonnées des séquences de points peuvent être retrouvées
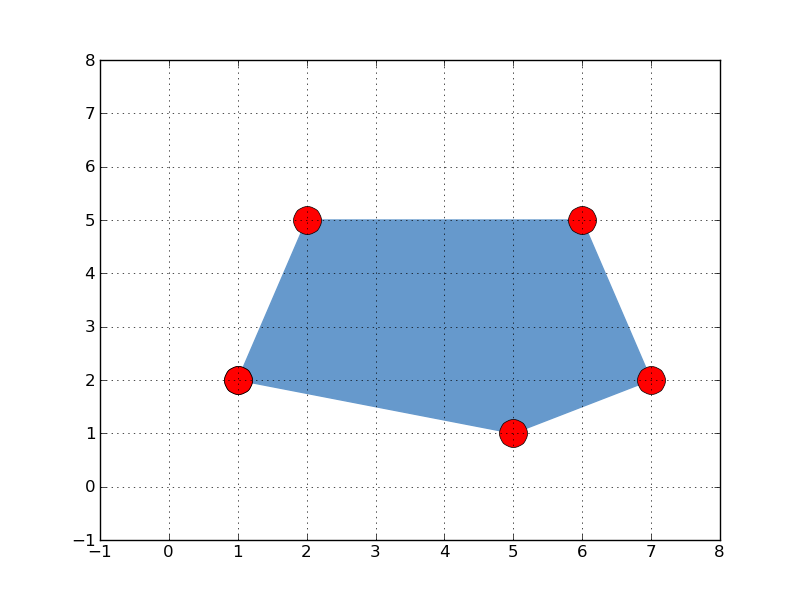
coord. points
- 3636 lectures
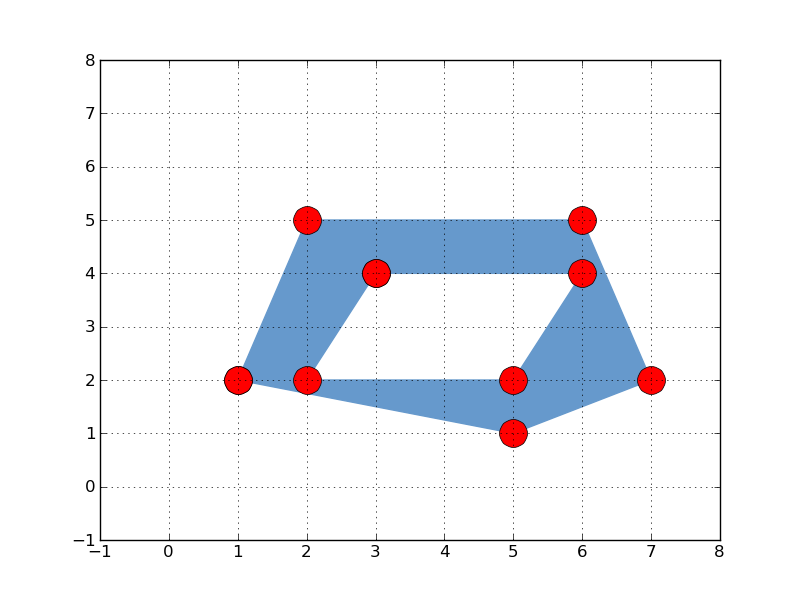
et un MultiPolygon qui est une collection de polygones
multipolygone
- 4533 lectures
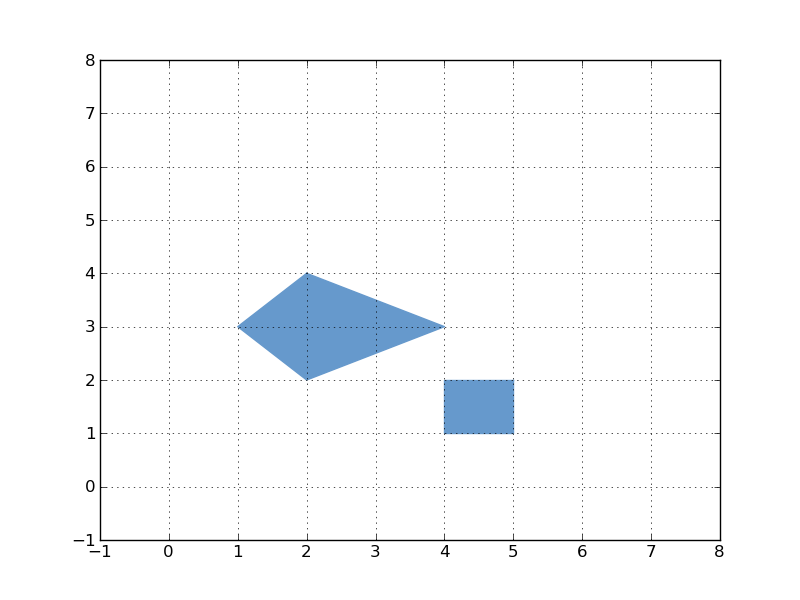
Le résultat des diverses opérations peut conduire à l'obtention d'objets hétérogènes associant diverses géométries. Cette classe de l'OGC est aussi implantée dans Shapely: GeometryCollection
GEOMETRYCOLLECTION (LINESTRING (210 380, 202.45283018867926 334.7169811320755),
LINESTRING (235 283.57142857142856, 260 280, 250 370, 210 380),
POLYGON ((235 283.57142857142856, 250 260, 160 230, 130 310, 180 370, 202.45283018867926 334.7169811320755, 235 283.57142857142856)))
Les "constructeurs" ou comment créer des nouvelles géométries à partir d'un objet géométrique existant (buffer, ...)
Shapely possède les contructeurs suivants:
- objet.buffer(distance, [résolution]): permet de créer des buffers positifs ou négatifs. Le terme résolution peut être utilisé pour préciser le nombre de segments de la géométrie résultante (voir script "polygone");
- objet.convex.hull (voir script "polygone")
- objet.enveloppe
- objet.simplify
- objet.boundary (voir script linearring - polygone)
- (objet.exterior ( réservé aux polygones, voir script linearring - polygone))
- objet.centroid
Les requêtes spatiales binaires (True, False) et les prédicats
Les relations spatiales entre géométries sont aussi normalisées par l'OGC. Elles se traduisent dans Shapely par des prédicats (fonctions renvoyant une valeur binaire, True ou False). Ils sont amplement expliqués dans le manuel de Shapely.
1) prédicats unaires, car ils s'appliquent à un seul objet géométrique
- objet.has_z¶
- objet.is_empty
- objet.is_ring (voir script "linearring -polygone")
- objet.is_simple
- objet.is_valid (voir script "polygones")
2) prédicats binaires, car ils s’appliquent à deux objets géométriques
- objet1.crosses(objet2) signifie que l'intérieur de objet1 recoupe l'intérieur de objet2, que objet1 ne contient pas objet2 et dont la dimension résultante doit être inférieure à celle des 2 objets;
- objet1.intersects(objet2) signifie qu'il y a une intersection entre les limites et les intérieurs des deux objets;
- objet1.touches(objet2) signifie que la limite de objet1 recoupe uniquement celle de objet2 mais qu'il n'y a pas d'intersection entre leurs intérieurs;
- objet1.within(objet2) signifie que l'intérieur et la limite de objet1 recoupent uniquement l'intérieur de objet2 (pas la limite);
- objet1.contains(objet2) signifie que l'intérieur et la limite de objet2 recoupe uniquement l'intérieur de objet1 et que leurs limites ne se touchent (touches)
- objet1.disjoint(objet2)
- objet1.equals(objet2)
- objet1.almost_equals(objet2)
Il en résulte, par exemple, qu'un polygone ne contient pas sa limite...(benjamin.chartier.free.fr/pro/)
Les requêtes spatiales D9-IM de l'OGC (matrice de Clementini)
Les résultats sont envoyés sous forme de matrice. C'est la matrice de Clementini ou notation DE-9IM (Dimensionally Extended Nine-Intersection Model de l' OGC, voir benjamin.chartier.free.fr/pro/ , postgis.org/documentation/manual-svn/ch04.html#DE-9IM )
- objet1.relate(objet2)
Nous allons construire cette matrice dans le point suivant. Notons que Sean Gillies a aussi développé un module d9im pour traiter ces relations.
L'analyse spatiale ou comment créer de nouveaux objets à partir de deux objets géométriques existants (union, intersection...) avec application à la matrice de Clementini
Shapely fournit aussi les méthodes permettant de visualiser ces relations spatiales en créant de nouvelles géométries (résultats de l'union, de l'intersection, de la différence ou de la différence symétrique entre 2 objets)
- object1.intersection(objet2)
- objet1.difference(objet2)
- objet1.symmetric_difference(objet2)
- objet1.union(objet2)
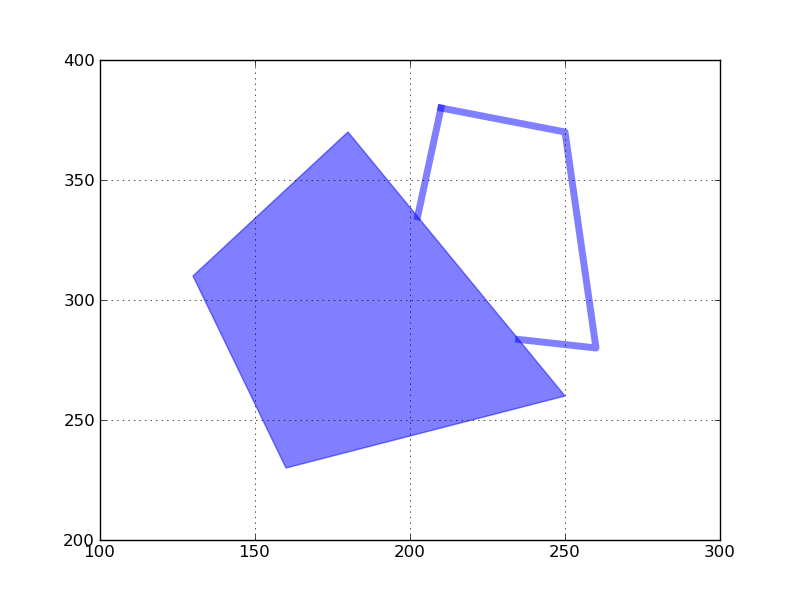
Pour illustrer toutes ces commandes, nous allons construire la matrice de Clementini pour caractériser l'intersection entre les 2 polygones suivants:
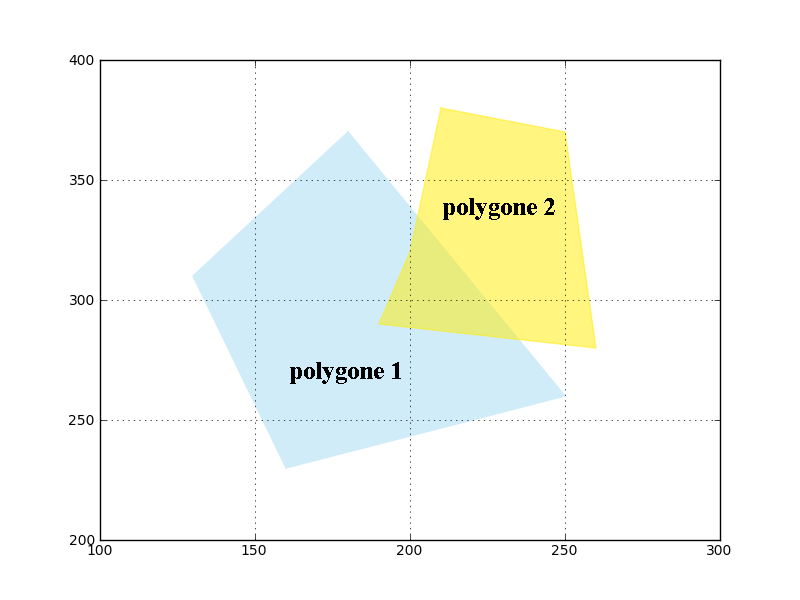
Le résultat obtenu est
Mais qu'est ce que cela signifie ? En fait, les chiffres obtenus correspondent à des dimensions d'objets. La matrice est en effet construite de la manière suivante:
Intérieur(Polygone 2) Limite(Polygone 2) Extérieur(Polygone 2)
______________________________________________________________________
Intérieur(Polygone 1) dimension(inters.) dimension(inters.). dimension(inters.)
Limite(Polygone 1) " " "
Extérieur(Polygone 1) " " "
Cette matrice est construite ici avec les méthodes d'analyse de Shapely:
.png)
lignes.png)
seul.png) dim = 2 dim = 1 dim = 2
dim = 2 dim = 1 dim = 2
lignes.png)
.png)
ligneseul2.png) dim = 1 dim = 0 dim = 1
dim = 1 dim = 0 dim = 1
seul.png)
lignes2.png)
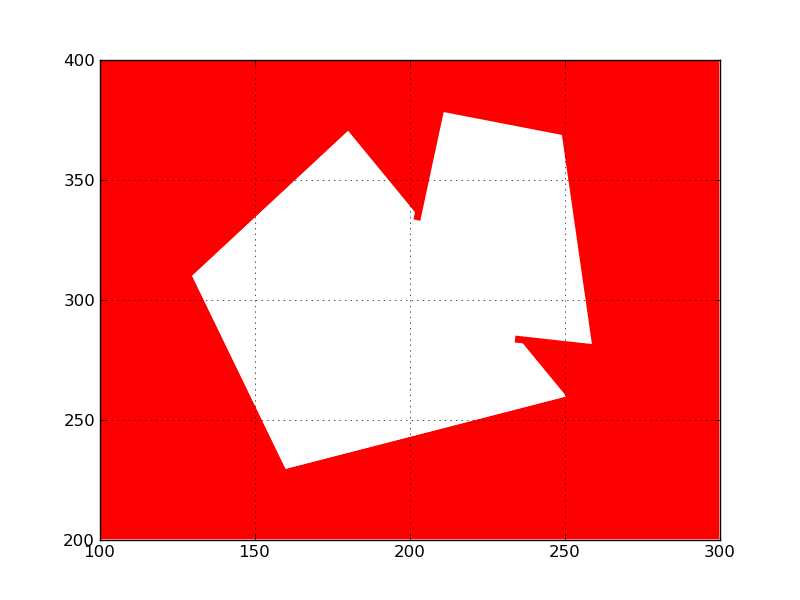 dim = 2 dim = 1 dim=2
dim = 2 dim = 1 dim=2
Le résultat est donc:
2 1 2
1 0 1
2 1 2
ou 212101212 conforme à ce qui a été obtenu par polygon1.relate(polygon2)
Quel est l'intérêt d'une telle démarche ? Celle de pouvoir créer des filtres spatiaux très précis pour rechercher des relations impossibles à obtenir par les méthodes traditionnelles. Par exemple, si je veux obtenir toutes les intersections de type "ligne dans polygone" (ligne 1, colonne 2 et ligne 2, colonne 1 de la matrice), je vais utiliser un filtre du genre "¨*1*1***** ". Cette méthode et surtout utilisée pour les les recherches dans les bases de données spatiales:
-- Identify road segments that cross on a line
SELECT a.id
FROM roads a, roads b
WHERE a.id != b.id
AND a.geom && b.geom
AND ST_Relate(a.geom, b.geom, '1*1***1**');
(tiré de postgis.org/documentation/manual-svn/ch04.html#DE-9IM )
Chritian Strobl explique tout cela dans gis.hsr.ch/wiki/images/3/3d/9dem_springer.pdf avec des matrices pour de nombreux cas.
Les applications pratiques (shapefiles, PostGIS, projections , autre traitement mathématique)
Tout ça, c'est bien beau, me direz-vous, mais cela reste apparemment purement théorique. Et non, car en pratique Shapely peut être utilisé pour traiter beaucoup de choses, des shapefiles, des résultats obtenus par des requêtes spatiales provenant des bases de données ou des traitements mathématiques divers.
En pratique, la démarche consiste toujours à transformer les objets en géométries Shapely pour pouvoir faire ensuite les traitements.
Pour un shapefile, la démarche a déjà été partiellement expliquée partiellement dans www.portailsig.org/content/python-visualiser-et-traiter-des-donnees-spatiales-de-type-xyz-shapefiles-ou-mnt-srtm. Sachant que la commande geom_type permet d'obtenir le type de géométrie d'un objet:
on peut effectuer le traitement avec le module ogr:
Shapely-ogr
- 4120 lectures
ou avec le module shpUtils (voir www.portailsig.org/content/python-et-les-shapefiles et www.aaronland.info/weblog/2009/04/12/hammock/):
Shapely-shpUtils
- 4168 lectures
Avec PostGIS les démarches ont été expliquées dans sgillies.net/blog/531/the-shapely-alchemist/ ou ici avec une adaptation du script "requête SELECT avec SQLObject" de www.portailsig.org/content/python-les-bases-de-donnees-geospatiales-2-mapping-objet-relationnel-orm-sqlalchemy-sqlobjec
résultats obtenus directement avec PostGIS en SQL:
directement avec PostGIS
- 3738 lectures
résultats obtenus avec SQLObject et Shapely:
Shapely - SQLObject - PostGIS
- 4183 lectures
Le SRID n'est pas pris en compte avec Shapely, mais hackmap.blogspot.com/2008/03/ogr-python-projection.html montre comment utiliser le module ogr pour le faire:
Shapely - ogr- projections
- 3806 lectures
Le manuel et la distribution fournissent de nombreux autres exemples comme la procédure pour découper des lignes en tronçons suivant une distance déterminée (gispython.org/shapely/docs/1.2/manual.html#linear-referencing-methods).
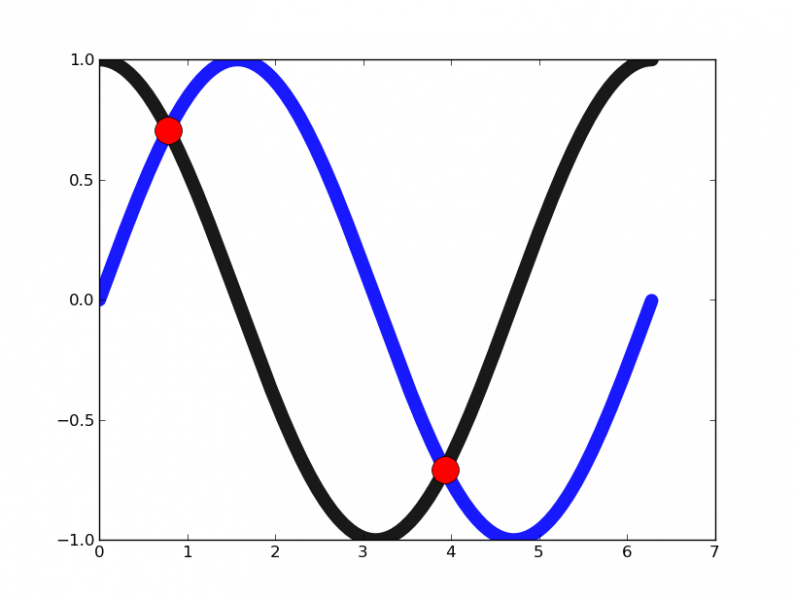
Mais Shapely peut aussi être utilisé à toute autre chose que le domaine spatial comme l'illustre cette réponse de plxpy sur www.developpez.net/forums/d755595/autres-langages/python-zope/general-python/points-intersection-courbes/ suite à une question pratique:
"Une petite démo pour calculer les intersections entre sinus et cosinus dans [0,2*pi]" (script original légèrement modifié)
traitement
- 3359 lectures
Comment dessiner les géométries avec matplotlib (classe Plot_Shapely)
En pratique, Shapely utilise des tableaux (array) numpy pour représenter les objets:
Shapely - array numpy
- 3924 lectures
Ces arrays numpy sont directement utilisables par matplotlib:
dessine points, lignes
- 3915 lectures
Cela marche aussi pour les limites des polygones, mais pas pour les aires (hormis en utilisant la commande pylab.fill). Matplotlib offre d'autres commandes pour figurer des surfaces, bien illustrées dans sgillies.net/blog/1013/painting-punctured-polygons-with-matplotlib/. Sur cette base Seans Gillies a développé un module spécifique pour le faire, descartes.
dessine aire
- 3412 lectures
Je me suis donc créé sur ces bases une classe Plot_shapely qui me permet de dessiner toutes les géométries (diagramme obtenu avec Yuml - yuml.me/edit/37c88fdd )

Classe
- 3341 lectures
Conclusions
Shapely est, pour moi, un magnifique outil pour celui qui aime Python et veut comprendre ce que l'on fait réellement avec un SIG ou une base de données spatiale qui respectent les normes de l' OGC.
Bien sur, il ne gère pas les données alphanumériques associées aux géométries, de même que les règles topologiques propres à certains logiciels. Ce devrait être possible en lui associant des modules comme ogr mais, cela reste purement théorique et ce n'est pas le but du module.
J'espère que cette introduction vous donnera les clés pour « jouer » avec Python et Shapely, ce qui reste pour moi le plus grand plaisir. Sean Gillies montre surtout comment une bonne connaissance de Python permet d'optimiser n'importe quel script pour n'importe quel logiciel.
Tous les traitements ont été effectués sur Mac OS X avec Python 2.5.4, diverses versions de Shapely suivant l'évolution du module (dernière 1.2), matplotlib, descartes et autres modules Python, Yuml, directement à partir de Python, et Inkscape pour la seule figure non matplotlib.
 Site officiel :
Shapely
Site officiel :
Shapely  Site officiel :
matplotlib
Site officiel :
matplotlib  Site officiel :
descartes
Site officiel :
descartes  Site officiel :
d9im
Site officiel :
d9im  Site officiel :
GEOS
Site officiel :
GEOS  Autres Liens :
manuel Shapely 1.05
Autres Liens :
manuel Shapely 1.05  Autres Liens :
manuel Shapely 1.2
Autres Liens :
manuel Shapely 1.2 
Commentaires
Une petite erreur
Hello,
Merci pour cette présentation, mais il y a une petite erreurs:
LinearRing n’étends pas Polygon mais LineString.
Je trouve également que les illustrations en dessus et en dessous de la phrase « Un polygone s.s. peut être défini comme une aire simple ou en « anneau » (« troué »). Il est défini par une ou des séquences ordonnées de points. » supère que les polygones sont plein et les mutipolygones sont troué, mais les deux peuvent être troué !
CU
Stéph
Vous n'avez pas bien lu et
Vous n'avez pas bien lu et ce n'est pas une petite erreur
"Les limites extérieures et intérieures d'un polygone sont des lignes fermées. C'est pourquoi le concept de LinearRing a été introduit par l'OGC pour les différencier des LineString. Dans Shapely, Sean Gillies en fait bien une sous-classe de Polygon."
C'est de la topologie; Dans les shapefiles, les géométries de PostGIS ou d'Oracle Spatial, lignes et polygones (LinearStrig et LinearRing) sont 2 géométries/topologies différentes. Une surface est constituée d'un contour et d'une aire, un contour (LinearRing) délimite toujours une aire, et une aire est toujours limitée par un contour, et ceci n'a rien à voir avec une ligne (LineString).
C'est pourquoi Sean Gillies l'a bien inclus dans sa classe Polygon, même si son implémentation pratique utilise la classe Point et la classe LineString.
Or le diagramme de classe s'adresse au module Shapely.
Poster un nouveau commentaire