PyQGIS: des géométries, des vecteurs, de l'algèbre vectorielle ou des cosinus directeurs, exemples d'applications.

	Niveau	Intermédiaire
	Logiciels utilisés	Quantum GIS (QGIS)
	Plateforme	Windows | Mac | Linux | FreeBSD

Après avoir présenté les algorithmes et les  fonctions en Python dans la première partie, PyQGIS: des géométries, des vecteurs, de l'algèbre vectorielle ou des cosinus directeurs..., nous allons en appliquer certains pour illustrer quelques applications sur un plan 2D avec PyQGIS à partir des diverses questions/réponses fournies par moi et d'autres sur le ForumSIG et sur gis stackexchange:

• comment créer une ligne à partir d'un point et un azimut (cosinus directeurs);
• comment créer des points équidistants sur une ligne (normalisation, multiplication ou cosinus directeurs);
• comment trouver le point médian sur une ligne ou un segment de ligne (somme, multiplication);
• comment découper une ligne en segments équidistants (normalisation, multiplication, somme, cosinus directeurs);
• comment obtenir l'azimut d'une ligne (azimut d'un vecteur);
• comment calculer l'angle entre 2 lignes (produit scalaire);
• comment calculer la distance minimum entre un point et une ligne (produit scalaire);
• comment obtenir la droite perpendiculaire entre un point et une ligne (produit scalaire).

Visualisation dans QGIS

Avant de commencer, il est nécessaire de pouvoir visualiser ces vecteurs/géométries dans QGIS de manière simple à partir de la console Python. Cela se fait en utilisant la particularité des « memory layers » (couches virtuelles, en mémoire).

Comme j'ai souvent besoin de créer des points et des lignes pour visualiser mes traitements à partir d'angles, j'ai créé une classe Python qui me permet d'effectuer simplement toutes les manipulations de création de couches et d'affichage dans QGIS (la classe complète me permet aussi de traiter les géométries Shapely dans QGIS et d'ajouter/modifier des éléments dans les tables attributaires):

#!/usr/bin/python
# encoding: utf-8
"""
QGIS: fonction et classe permettant de créer des couches virtuelles
(memory layers)
Martin Laloux 2012
"""
from qgis.core import *
 
class Crea_couche(object):
    """création d'une couche virtuelle (memory layer) de type Point, LineString
    ou Polygon,ajout des géométries et affichage"""
    # création de la virtuelle à partir du nom et du type géométrique
    def __init__(self,nom,type):
         self.type=type
         self.nom = nom
         self.couche =  QgsVectorLayer(self.type, self.nom , "memory")
         self.pr = self.couche.dataProvider() 
    def create_point(self,point):
	#ajout d'un point
        self.seg = QgsFeature()
        self.seg.setGeometry(QgsGeometry.fromPoint(point))
        self.pr.addFeatures([self.seg])
        self.couche.updateExtents()
    def create_ligne(self, point1,point2):
	#ajout d'une ligne
        self.seg = QgsFeature()
        self.seg.setGeometry(QgsGeometry.fromPolyline([point1,point2]))
        self.pr.addFeatures( [self.seg] )
        self.couche.updateExtents()
    def create_poly(self,points):
	#ajout d'un polygone
        self.seg = QgsFeature()  
        self.seg.setGeometry(QgsGeometry.fromPolygon([points]))
        self.pr.addFeatures( [self.seg] )
        self.couche.updateExtents()
    @property
    def aff_couche(self):
	#fin de l'édition et affichage  de la couche
        QgsMapLayerRegistry.instance().addMapLayers([self.couche])
 

Ce qui permet, en plaçant ce script dans le path de Python (PYTHONPATH):

from crea_mem_layer import Crea_couche
# création d'une couche point
pt = Crea_couche("points", "Point")
# ajout d'un point à la couche
line_start = QgsPoint(50,50)
pt.create_point(line_start)
# ajout d'un autre point à la couche
line_end = QgsPoint(100,150)
pt.create_point(line_end)
# fin de l'édition et affichage de la couche
pt.aff_couche
# création d'une couche ligne
li = Crea_couche("ligne", "LineString")
# ajout d'une ligne à la couche
li.create_ligne(line_start,line_end)
# fin de l'édition et affichage de la couche 
li.aff_couche
# création d'une couche polygones
pol = Crea_couche("poly", "Polygon") 
points = [QgsPoint(60,60),QgsPoint(60,80),QgsPoint(80,80),QgsPoint(80,60),QgsPoint(60,60)] 
pol.create_poly(points) 
# fin de l'édition et affichage de la couche 
pol.aff_couche

Résultats dans QGIS:

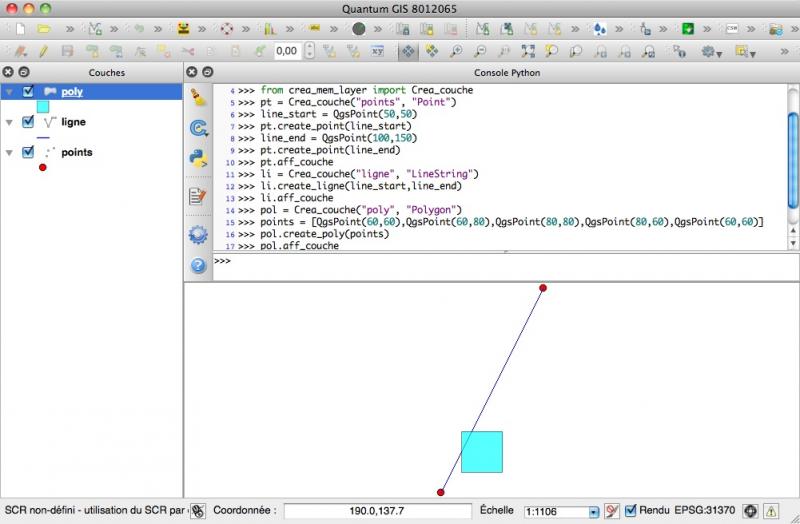
Nous voici armés pour appliquer les algorithmes et fonctions de géométrie vectorielle analysés dans le précédent article et résumés dans le script algèbre_vect_PyQGIS.py.

Exemples d'applications

Comment créer une ligne à partir d'un point et un azimut ? (cosinus directeurs)

Il est possible, comme souvent enseigné, d'utiliser la transformation des coordonnées cartésiennes en coordonnées polaires (voir point suivant), mais c'est beaucoup plus direct d'utiliser les cosinus directeurs (cosdir_azim(azimut)) qui renvoient un vecteur unitaire. Il suffit donc de le multiplier par la longueur voulue (voir [QGIS] Créer des points autour d'un autre point aux coordonnées connues).

À partir de la ligne obtenue par le traitement précédent (line_start, line_end):

# calcule la position du point situé à une distance  et un  azimut du point p
azimut = 120
longueur = 50
# cosinus directeurs de l'azimut
cosa, cosb = cosdir_azim(azimut)
# point résultant
resultat = QgsPoint(point.x()+(longueur*cosa), point.y()+(longueur*cosb))
# création des couches point et ligne résultantes
pt = Crea_couche("pt_120_50", "Point")
pt.create_point(resultat) 
pt.aff_couche
li = Crea_couche("l_120_50", "LineString")
li.create_ligne(line_end,resultat)
li.aff_couche

Résultat: 

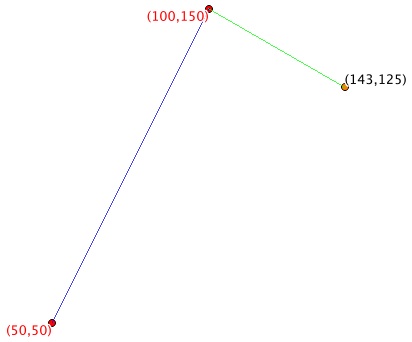
Et une simple boucle permet de continuer le cheminement éventuel:

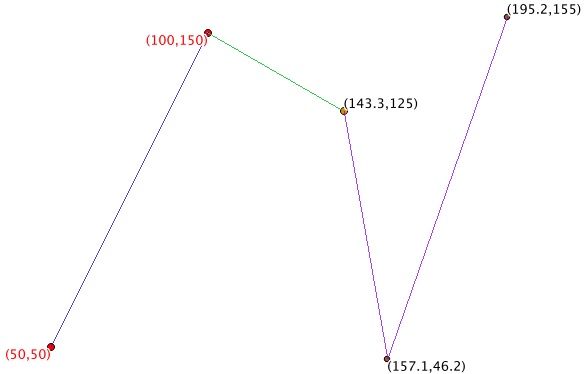
Comment créer des points équidistants sur une ligne (normalisation, multiplication ou cosinus directeurs)

Ici, les utilisateurs de Shapely sont avantagés, car ils disposent d'une fonction pour générer des points équidistants sur une ligne (ligne.interpolate(distance), voir How to create equidistant points in QGIS?. C'est dans la continuité du point précedent.

Le nouvel API Python de la version master dispose aussi d'une telle fonction geom.interpolate(distance), voir Generating chainage (distance) nodes in QGIS de Nathan Woodrow (avec les « lourdeurs » de PyQGIS). Il est tout aussi facile de les créer directement en utilisant l'algèbre vectorielle:

Générer des points équidistants

1. par normalisation et multiplication

Le principe est simple, puisque suivant la conception retenue, un vecteur « point » a une direction (si je veux changer l'angle, voir le point précédent), il suffit donc de:

1. calculer le vecteur unitaire (normalisation, fonction normpt(point));
2. le multiplier par n fois l'intervalle voulu (fonctions vecxscal(point, k) et som(point1, point2)).

# vecteur unitaire: normalisation du vecteur
point = QgsPoint(50,50)
norme= normpt(point)
serie = Crea_couche("normalisation", "Point")
#  ajout de 10 fois du vecteur normalisé x i
for i in range(5,100,5):
    serie.create_point(som(point,vecxscal(norme,i)))
serie.aff_couche(pt_layer)

2. par les cosinus directeurs

Mais il est beaucoup plus intuitif de le faire avec les cosinus directeurs (qui renvoient un vecteur unitaire, pour mémoire) mais, cette fois-ci, à partir des coordonnées cartésiennes (cosdir(point)):

# cosinus directeur du point de départ
cosa,cosb = cosdir(point)
# traitement
serie = Crea_couche("cosdir", "Point")
# points équidistants de 5 m sur une longueur de 100 m
for i in range(5,100,5):
    serie.create_point(QgsPoint(point.x()  + (i * cosa), point.y() + (i*cosb)))
serie.aff_couche

 Résultat:

Générer des points équidistants sur une ligne:

Dans le cas de points générés sur une ligne, il y a une composante supplémentaire qui intervient, la longueur de la ligne. Les points générés doivent être situés sur la ligne et limités par sa longueur:

Application sur une polyligne QGIS existante:

couche = qgis.utils.iface.activeLayer()
def paires(list):
    # Itération par paires dans une liste
    for i in range(1, len(list)):
        yield list[i-1], list[i]
intervalle = 5
# création de la couche virtuelle
pt_mid  = Crea_couche("mid5", "Point")
#traitement sur les éléments sélectionnés
for elem in couche.selectedFeatures():
    ligne = elem.geometry()
    for seg_start, seg_end in paires(ligne.asPolyline()):
       line_start = QgsPoint(seg_start)
       line_end = QgsPoint(seg_end)
       # point médian du vecteur ligne
       pointm =diff(line_end, line_start)
       # cos directeurs de la ligne
       cosa,cosb = cosdir(pointm)
       # longueur du vecteur (ligne)
       long = dist(line_end, line_start)
       for i in range(intervalle,long,intervalle):
             pt_mid.create_point(QgsPoint(line_start.x()  + (i * cosa), line_start.y() + (i*cosb)))
pt_mid.aff_couche

Si la longueur de la ligne n'est pas un multiple de l'intervalle, il est possible de choisir entre un dernier segment inférieur à l'intervalle (à gauche) ou supérieur à l'intervalle (à droite):

.

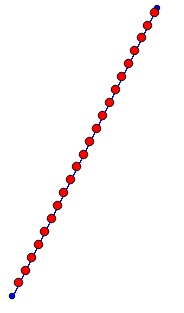
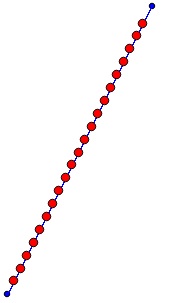Tant avec la fonction de Shapely, avec celle du nouvel API de PYQGIS  ou avec celle présentée ici, il est possible de constater quelques petits problèmes comme ceux rencontrés au sommet supérieur:

polyligne,             avec l'algorithme proposé,               avec Shapely

C'est lié au fait que la boucle traite les résultats par segments et non sur l'entièreté de la ligne. Si l'on veut corriger le tir, il serait nécessaire de travailler sur la longueur totale de la polyligne.

Comment découper une ligne en segments équidistants

La réponse est évidente, il suffit de transformer les résultats précédents en lignes (de point à point).

Comment trouver le point médian sur une ligne ou un segment de ligne (somme, multiplication):

Cela peut se faire avec le plugin Sextante (algorithmes fTools) mais, il est intéressant de présenter l'algorithme avec les fonctions som(point1, point2) et vecxsal(point, k) car il permet de trouver d'autres points que le point médian sur une ligne (il suffit de modifier la valeur k).  Je vous invite à consulter ma réponse sur gis.stackexchange à How to find the middle point of a line in QGIS:

def mid(point1, point2):
      return vecxscal(som(point1,point2),0.5) 

L'inverse, comment obtenir l'azimut d'une ligne

Cela pourrait se faire en insérant dans un champ de la calculatrice de champs (voir How to add Direction and Distance to attribute table?):

(atan((xat(-1)-xat(0))/(yat(-1)-yat(0)))) * 180/3.14159 + (180 *(((yat(-1)-yat(0)) < 0) + (((xat(-1)-xat(0)) < 0 AND (yat(-1) - yat(0)) >0)*2)))

mais si une ligne est composée de plusieurs segments, le résultat sera l'azimut moyen des segments. Si l'on veut les azimuts de tous les segments, il faut découper la ligne en segments et utiliser la fonction azimut(point1, point2).

Pour un traitement complet, je vous invite à consulter mes réponses sur gis.stackexchange à How do I find vector line bearing in QGIS or GRASS? et How to add Direction and Distance to attribute table? à partir de polylignes.

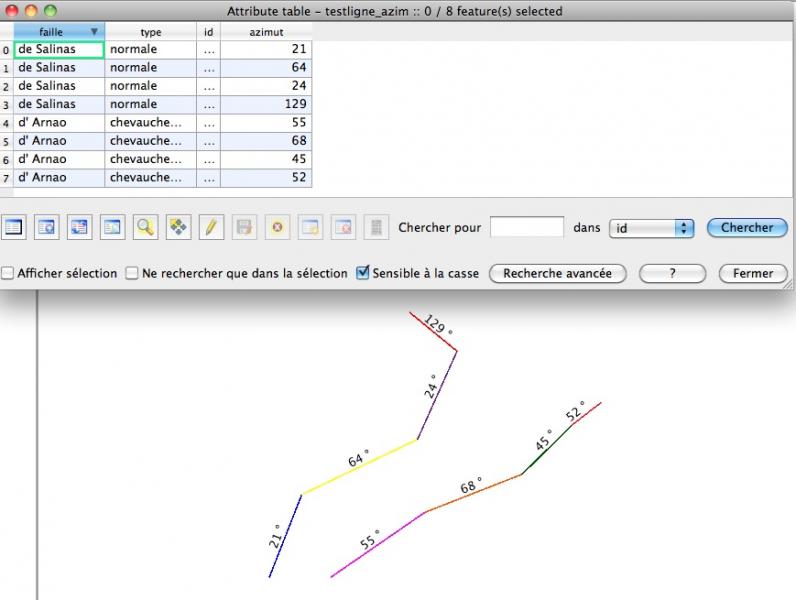
Comment calculer l'angle entre 2 lignes (produit scalaire):

Cela a été vu avec le produit scalaire entre vecteurs (dot_product(point1, point2)) ou avec la différence entre les azimuts des 2 vecteurs, voire avec le déterminant.

Comment obtenir la droite perpendiculaire entre un point et une ligne et/ou calculer la distance minimale entre un  point et une ligne (produit scalaire).

Le problème posé sur How to draw perpendicular lines in QGIS? était « comment trouver  la ligne perpendiculaire entre le point bleu et la ligne rouge et sa longueur ? »:

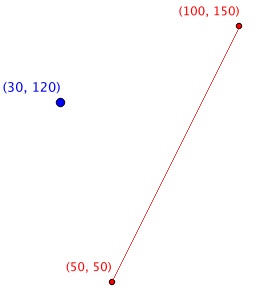
La  solution a été donnée par Paul Bourke (Minimum Distance betweena Point and a Line? ) en utilisant le produit scalaire et ces propriétés d'orthogonalité. Cette distance est en effet la longueur du vecteur perpendiculaire depuis ce point vers la ligne ou le segment de ligne. (voir  ma réponse à How to draw perpendicular lines in QGIS?) . Cela se fait avec le carré de la distance ( fonction sqrDist de PyQGIS):

def distance_min_point_ligne(point, line_start, line_end):
     # Calcul de la distance minimale entre un point et un segment de ligne et intersection
     # sqrDist de la ligne (fonction PyQGIS = longueur) de la ligne **2)
     distcar = line_start.sqrDist(line_end) 
     # distance minimale
     u = ((point.x() - line_start.x()) * (line_end.x() - line_start.x()) + (point.y() - line_start.y()) * (line_end.y() - line_start.y()))/(distcar)
     # point d'intersection sur la ligne
     ix = line_start.x() + u * (line_end.x() - line_start.x())
     iy = line_start.y() + u * (line_end.y() - line_start.y())
     return QgsPoint(ix,iy)

 et le traitement (après avoir créé une couche avec un point de coordonnées (30,120):

#création de la ligne perpendiculaire
li = Crea_couche("perp", "LineString")
li.create_ligne(point,distance_min_point_ligne(point, line_start, line_end))
li.aff_couche(line_layer)
# distance minimale (longueur de la ligne résultante)
sqrt(point.sqrDist(distance_min_point_ligne(point, line_start, line_end)))
49.193495504995376

Résultat:

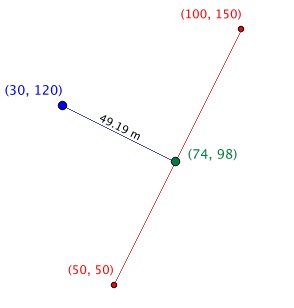
<br>

La preuve de l'orthogonalité est fournie par le résultat du produit scalaire entre les 2 vecteurs:

point_res = distance_min_point_ligne(point, line_start, line_end)
point_res
(74,98)
dot_product(diff(point,point_res), diff(line_end,line_start))
 0

D'autres solutions ont été proposées comme celles de Nearest neighbor between a point layer and a line layer ou Elevation profile 10 km each side of a line avec Shapely.

Et tout le reste...

Et ce n'est pas tout, car avec l'algèbre vectorielle vous pouvez traiter beaucoup d'autres choses, comme les unions, les intersections, etc. (mais c'est déjà disponibles de manière standard dans la plupart des logiciels SIG), toutes les transformations angulaires comme les rotations ou les changements d'axes ou de système de projection. Il est même possible de traiter les géométries 3D avec le module shapely, comme illustré sur le Portail dans QGIS, représentation 3D des couches vectorielles (shapefiles dits 3D ou shapefiles avec attributs z) avec les modules Python Matplotlib ou Visvis à partir de la console Python ou des photos d'objets 3D comme le montre l'article récent DigiFract: A software and data model implementation for flexible acquisition and processing of fracture data from outcrops de N.J. Hardebol et G. Bertotti, 2013, Computers & Geosciences, v. 54, p. 326–33, qui utilise QGIS et l'algèbre vectorielle avec le module Shapely pour traiter des photos de parois ou d'affleurements géologiques (je vous conseille d'aller examiner les figures, librement disponibles pour comprendre la démarche).

Conclusions

J'espère que ces quelques traitements vous auront donné ou redonné l'envie d'utiliser l'algèbre vectorielle et, surtout,  l'envie d'aller « farfouiller » ailleurs, car, comme l'a souligné Sean Gillies, le traitement des données spatiales n'a rien de particulier vis-à-vis des autres types de données (« I want it to refute the notion that "spatial is special" and have no gotchas, no surprise » Fiona makes reading and writing data boring), hormis la complexité des explications...

Cela n'est pas limité aux vecteurs. À titre d'exemple, je voulais tester une méthode de lissage d'une couche par courbes de Bézier, méthode non disponible dans QGIS. Une rapide recherche m'a conduit à bezier_smooth.py de Matthew Perry (perrygeo) et à moi les courbes de Bézier cubiques ou quadratiques (en rouge sur la figure) avec la possibilité d'utiliser des points de contrôle (programmés):

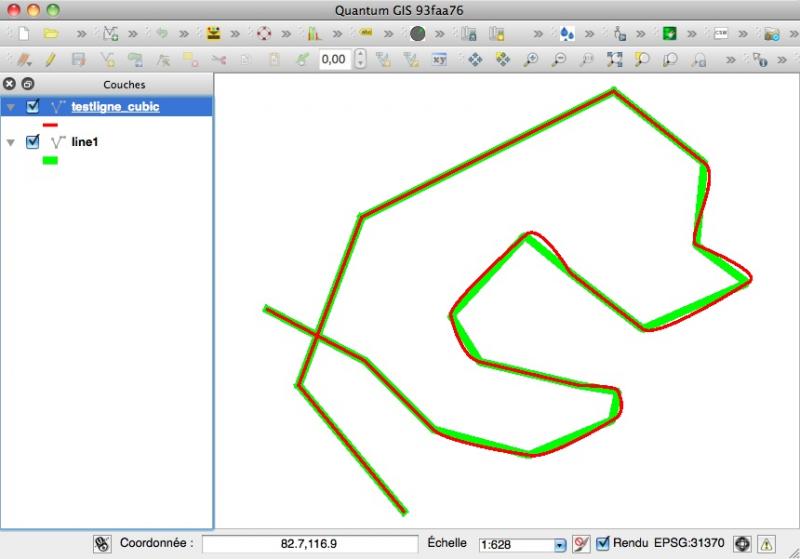
Mais, il est vrai que du fait de mon travail, j'accorde plus d'importance aux géométries qu'aux traitements géomatiques classiques et que la connaissance préalable du module Shapely facilite grandement les choses (il est beaucoup plus clair pour les traitements, de même que le module gvsig de gvSIG, voir gvSIG 2.0: Scripting, exploit your gvSIG (III): Generate a polygon from a course ).

Pourquoi ne pas en faire un plugin, réclameront certains ?

Car tout ne peut pas être transformé en plugin, ma classe Python, spécialisée, me permet d'ajouter successivement des géométries sans passer par une interface graphique qui ralentirait le processus, ou d'utiliser un script Python. Je trouve aussi que l'utilisation de PyQt4 « obscurcit » tout...

Cela signifie aussi qu'un logiciel SIG comme QGIS peut être utilisé pour faire autre chose que de la géomatique pure, comme l'apprentissage de la géométrie, des vecteurs ou même, les traitements divers sur des images non géographiques, comme les photographies (utilisation en géologie (voir plus haut) ou en archéologie, par exemple, voir Exemple d’utilisation de Photoscan/QGIS pour la création d’un modèle géoréférencé 2.5D ).

Tous les traitements ont été effectués sur Mac OS X, avec le script crea_mem_layer.py (origine des figures) et plusieurs versions de QGIS master.

licence Creative Commons Paternité-Pas d'Utilisation Commerciale-Partage des Conditions Initiales à l'Identique Commerciale 2.0 France