Les statistiques directionnelles (ou pourquoi la moyenne de 350° et 10° n'est pas égale à 180°): introduction dans le domaine des SIGs (moyenne angulaire, interpolations angulaires, etc.)

Les valeurs angulaires (orientations/directions) sont implicites ou explicites dans toutes les relations spatiales (une ligne a une direction/orientation, un point peut être considéré comme un vecteur (voir PyQGIS: des géométries, des vecteurs, de l'algèbre vectorielle ou des cosinus directeurs... ) et enfin tout objet peut avoir un attribut angulaire). Leurs traitements sont peu abordés dans tous les ouvrages/cours/tutoriels francophones.

Et pourtant, si on essaye de leur appliquer les méthodes de calculs linéaires classiques, les résultats seront très étranges voire problématiques comme l'illustre la question posée sur le ForumSIG [QGIS 2.x] Interpolation de données angulaires.

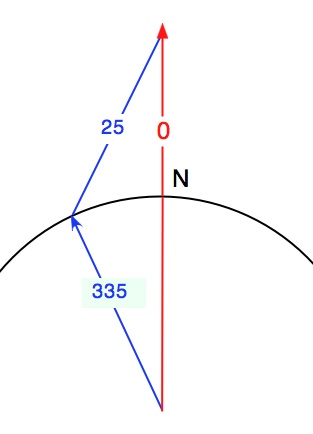
Prenons le simple cas d'un calcul de moyenne entre 2 azimuts de 335° et 25° avec le 0° situé au Nord.

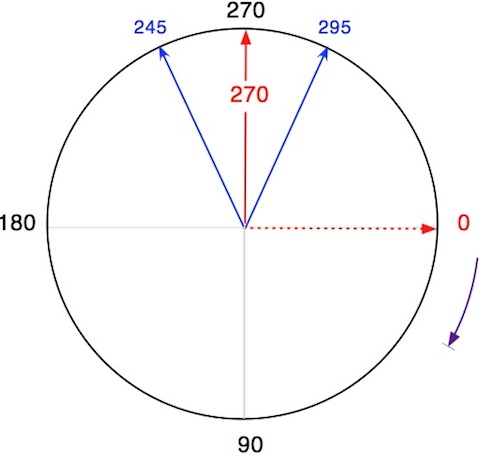
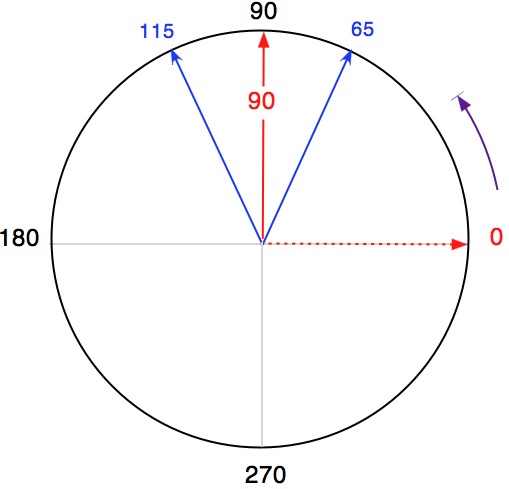
La réponse obtenue par les méthodes traditionnelles est de 180° ce qui n'est clairement pas ce à quoi on s'attend logiquement (la réponse attendue serait obtenue en réécrivant 335° comme -25°). Si la valeur d'origine (0°) est placée à l'Est (canevas mathématique) et qu'une rotation horaire est utilisée, les valeurs d'azimut deviennent 245° et 295° et le résultat sera la réponse attendue de 270°. Il en va de même avec une rotation antihoraire (90°).

Cet exemple simple permet donc de constater:

1. que les valeurs sont circulaires (et non linéaires), c'est-à-dire qu'elles se distribuent sur un cercle avec des valeurs comprises entre 0 et 360°, les valeurs 0° et 360° étant équivalentes (périodicité des mesures). Cela  va compliquer  beaucoup de choses comme le calcul d'interpolations, par exemple;
2. que les valeurs des différents moments statistiques (moyenne, écart type, ...) vont dépendre du choix arbitraire du point d'origine (0°) et du sens de rotation.

Les méthodes linéaires usuelles ne peuvent donc pas leur être appliquées. Il faut alors se tourner vers des techniques d'analyse invariantes au choix de l'origine et au sens de rotation et qui permettent de tenir compte du problème de périodicité. Ce sont les Statistiques directionnelles, domaine relativement récent, et peu développé en langue française (comparez avec la version anglaise de Wikipedia Directional statistics).

Je ne m'intéresserai ici qu'à la manière de traiter ce type de données dans le cas de traitements géomatiques comme les interpolations, et non à toute la partie statistique pure (types de distributions, uniforme, von Mises, Fisher, Bingham (3D), tests de conformités, Kuyper, Rayleigh, Watson-Williams, ...) en renvoyant vers les ouvrages cités pour aller plus loin. Elles sont indispensables si l'on veut sérier ou comparer des populations de données angulaires. Je présenterai le problème de la manière suivante:

Historique (bibliographie)
Classification des données angulaires (circulaires, sphériques, directionnelles, axiales)
Représentation
Traitements suivant le type de données (moments statistiques basiques)
En pratique, comment les interpoler ?

Je pars avec un avantage, car en tant que géologue, j'ai dû apprendre à pratiquer cette discipline lors de mes études pour le traitement des diverses mesures géologiques angulaires (directions, orientations, pendages, etc., voir QGIS et géologie structurale: création automatique de rosaces directionnelles et de canevas stéréographiques avec PyQGIS sur le Portail), mais dans un cadre non géomatique.

Historique (bibliographie)

Un petit historique bibliographique s'impose ici car les ouvrages de base, exclusivement consacrés au sujet, sont relativement peu nombreux et en anglais. De nombreuses méthodes avaient auparavant été proposées dans diverses revues scientifiques, mais de manière dispersée dans différents domaines.

• Statistics of Directional Data (1972) de K. V. Mardia, Academic Press, 357 pp. est le premier ouvrage qui en synthétise les principes mathématiques (complexes).
• Circular Statistics in Biology (1981) de E. Batschelet, Academic Press, 371 pp. les met en pratique dans un domaine spécifique;
• Statistical Analysis of Spherical Data (1987) de N. I. Fisher, T. Lewis, B. J. J. Embleton, Cambridge University Press, 329 pp. qui synthétisent les principes pour les données angulaires sphériques (3D);
  
• Spatial Data Analysis by Example, Vol 2: Categorical and Directional Data (1989) de G. J. G. Upton, B. Fingleton, Wiley, 432 pp., qui les mettent en pratique à plus grande échelle;
• Statistical Analysis of Circular Data (1993) de N. I. Fisher, Cambridge University Press, 295 pp., sans doute le plus connu. C'est le seul qui propose en effet des traitements d'analyse spatiale. Il a aussi donné son nom aux « Fisher Statistics».
• Directional Statistics (1999) de K.V. Mardia, P.E. Jupp , Wiley, 432 pp., mise à jour de l'ouvrage de 1972;
• Topics in Circular Statistics (2001) de S. R.Jammalamadaka, A. Sengupta World Scientific, 336 pp., le plus théorique, mais qui proposait des traitements en S/R avec le package CircStats qu'ils créent pour S;
• Circular Statistics in R (2013) de A. Pewsey, M. Neuhäuser, and G. D. Ruxton, Oxford University Press, 208 pp. le plus récent et le plus pratique, car il est une synthèse de tous les précédents ouvrages avec de nombreuses applications en R avec le package Circular (successeur de CircStats et plus complet)  et son site associé Circular Statistics in R où il est possible de télécharger les scripts R.

En français, je n'ai trouvé qu'un article qui aborde simplement et clairement le sujet:

•  Statistiques circulaires (pdf) (2005)  de C.Mello dans Quantitative Methods for Psychology, Vol. 1 (1), p. 11-17

Il y a bien entendu d'autres livres plus généraux ou des tutoriels qui abordent ces thèmes dans des chapitres ou des parties. Ces statistiques sont en effet utilisées dans tous les domaines scientifiques qui traitent de directions/orientations (cartographie, géologie, géophysique, paléomagnétisme, astronomie, physique, océanographie, météorologie, biologie, médecine, ...) et peuvent aussi être appliquées à l'analyse des phénomènes cycliques (comme la variation annuelle des précipitations, par exemple). Le dynamisme de cette discipline est illustré dans des congrès comme l'International workshop "Advances in Directional Statistics"   en 2014.

Classification

En pratique, il est possible de distinguer deux couples de classes de données directionnelles qui donnent lieu à quatre types distincts:

1. elles peuvent être en 2D (circulaires) comme la direction des vents, les linéaments, etc. ou en 3D (sphériques) comme les couches géologiques (direction et pendage). L'approche en 2D est celle qui intéresse les géomaticiens (cartes) alors qu'en tant que géologue, je m'intéresse plus à l'approche 3D (stéreonets, etc.);
2. elles peuvent se rapporter à l'orientation et/ou à la direction des  mesures:
   
   1. celles qui ont une direction (avec un sens) dont la valeur peut varier entre 0 et 360° (Statistiques circulaires, Circular statistics, Directional orientation data ou Circular orientation data  pour les auteurs anglo-saxons). Elles peuvent être représentées par des vecteurs (direction des vents, du mouvement d'un animal, par exemple);
   2. celles qui n'ont qu'une orientation dans un intervalle de 0 à 180° (puisque angle et angle + 180° sont équivalents, Axial data pour les auteurs anglo-saxons). Elles sont représentées par des lignes (linéaments, etc.).

Représentation

Depuis toujours ces données sont analysées par des méthodes graphiques (divers types d'histogrammes, de rosaces directionnelles, canevas stéréographiques (3D), etc.). Elles permettent de caractériser visuellement les distributions spatiales.

                                                 

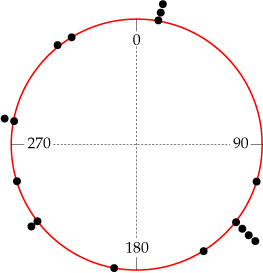
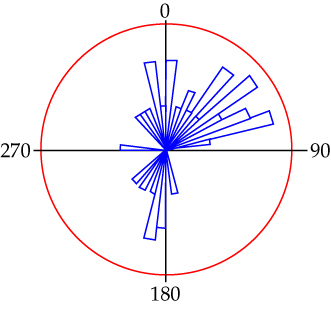
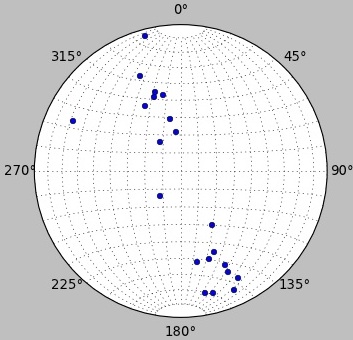
Bien qu'utiles, ces méthodes ont des limites (comme le choix de l'intervalle des rosaces qui est arbitraire). C'est pourquoi d'autres méthodes plus précises ont été élaborées.

Traitements suivant le type de données (moments statistiques basiques)

Une remarque s'impose ici, si les données sont toutes circonscrites à une région précise du cercle (de 0 à 180°, par exemple),  le problème de la périodicité ne se pose plus et elles peuvent être traitées comme des données linéaires, mais cette démarche est susceptible de poser d'autres problèmes statistiques. Mais si une seule des valeur est supérieure à 180°, la moyenne arithmétique donnera des résultats incorrects et il faudra utiliser les solutions qui vont être présentées.

Les données circulaires représentées par des vecteurs

La solution est d'utiliser les valeurs de direction comme des vecteurs (et non des scalaires) et d'utiliser les règles vectorielles. Comme les calculs ne concernent que les angles et pas les longueurs des vecteurs, ceux-ci sont simplifiés en vecteurs unitaires (de longueur 1, voir PyQGIS: des géométries, des vecteurs, de l'algèbre vectorielle ou des cosinus directeurs... pour la suite).

La direction moyenne est alors la direction de la simple somme des vecteurs. Dans le cas de l'exemple introductif, le résultat est bien celui qui est attendu, quels que soient le 0° et le sens de rotation choisis.

 

Dans le cas de plusieurs vecteurs:

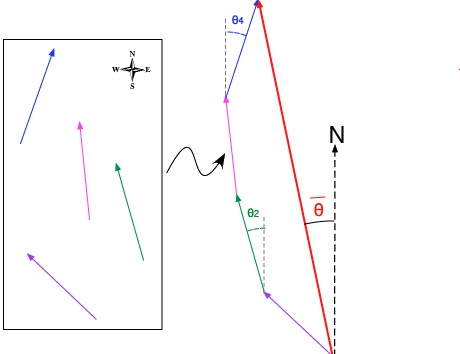
Une fois que l'origine (0°) et le sens de rotation (horaire ou antihoraire) ont été fixés, il est facile de les transformer en 2 (ou 3) coordonnées suivant les divers critères illustrés ci-dessous (l'important est de conserver les mêmes critères tout le long du processus). Tous les calculs se font sur ces coordonnées et non sur la valeur angulaire.

 

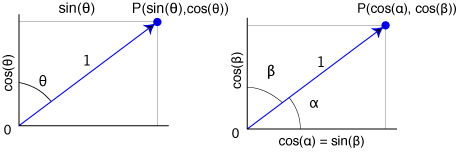
polaire                            cosinus directeurs

ou

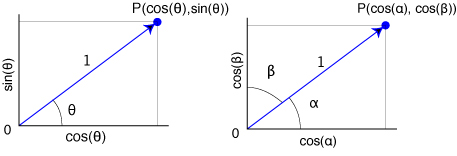
polaire                            cosinus directeurs 

En 3D ce sont les 3 cosinus directeurs qui seront surtout utilisés:

 

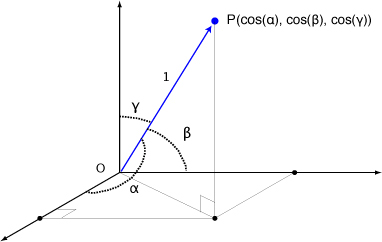
La direction moyenne est alors calculée par les règles trigonométriques classiques, c'est:

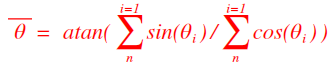
avec toutes les règles inhérentes aux arc tangentes (il faut être attentif aux signes de sin(Ɵ) et cos(Ɵ). Il vaut mieux utiliser la fonction atan2).

Une valeur intéressante est donnée par la longueur résultante moyenne (avec n valeurs):

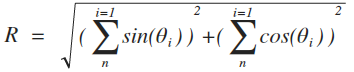
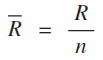
Elle varie  de 0 à 1 (= 1 signifie que tous les vecteurs ont la même direction) et constitue une mesure de la dispersion analogue à la variance classique. Il est possible d'en déduire:

• la variance circulaire classique  = 1- longueur résultante moyenne;
• la variance circulaire sensu Batschelet (1981) = 2 * (1- longueur résultante moyenne).

C'est cette dernière définition de la variance qui est utilisée dans le package Circular. Il est évidemment possible d'aller plus loin en calculant l'écart-type angulaire, le coefficient de dissymétrie (skewness), le kurtosis, etc.

Seul ArcGIS propose une commande standard pour calculer ces paramètres: Linear Directional Mean (Statistiques spatiales) et le processus est expliqué dans Fonctionnement de Linear Directional Mean. Le résultat sera une nouvelle couche (le vecteur "moyen" en rouge):

avec comme attributs:

CompassA est la direction moyenne par rapport au N, DirMean est la direction moyenne dans le canevas mathématique (E), CirVar est la variance circulaire, le reste sont des moyennes linéaires diverses (AveLen étant la moyenne des longueurs). A titre de comparaison, je vous fourni les procédures en R avec Circular (avec circular.R) et en Python (stats_circulaires.py ) pour ces mêmes données. Seules les lignes peuvent être traitées avec la fonction d'ArcGIS, ce qui n'est pas le cas avec les autres solutions (points avec attributs angulaires par exemple).

Je ne connais pas de fonction équivalente dans QGIS, GRASS GIS, gvSIG et autres, mais c'est facile à implémenter en R ou Python.

Les données axiales (orientation)

Elles représentent un autre type de problème. Elles sont différentes des données circulaires s.s. du fait que l'angle et l'angle + 180° représentent la même orientation (de plus, l'intervalle 180° est choisi arbitrairement). Comme déjà dit, n'étant pas circulaires, elles pourraient être traitées comme des données linéaires, mais depuis Mardia (1972), l'approche standard est de doubler les angles (modulo 360°, c'est à dire que pour une valeur de 340° -> 680° -> 680° - 360° = 320° alors que 140° -> 280° ) et obtenir ainsi des données circulaires similaires aux précédentes. Les résultats finaux seront ajustés en conséquence (direction moyenne / 2, par exemple. En fait, cette méthode a été proposée dès 1939 par W.C. Krumbein dans Preferred orientation of pebbles in sedimentary deposits. Journal of Sedimentary Petrology, 47, 673-706).

ArcGIS, toujours avec Linear Directional Mean (Statistiques spatiales), permet aussi de les traiter (lignes seulement), mais les résultats diffèrent de ceux obtenus par l'approche standard.

Et les longueurs ?

Jusqu'à présent, seules les directions/orientations ont été considérées et pas les longueurs des objets. Comme ce sont des données linéaires, tous les traitements traditionnels peuvent leur être appliqués.  Mais cela veut aussi dire qu'une ligne de 100 km a le même poids qu'une autre de 1m dans les calculs statistiques. Certains auteurs proposent alors de pondérer les résultats par les longueurs des lignes, mais ce sont des considérations purement statistiques.

En pratique, comment les interpoler ?

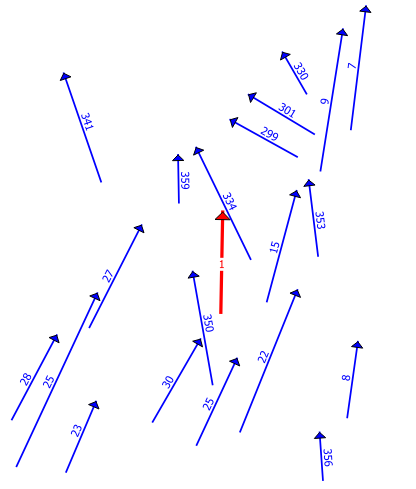
Un bel exemple a été récemment proposé par Riccardo Klinger dans  How to create a wind map in QGIS suite de How to create a wind map in ArcGIS. Les données de départ sont des valeurs directionnelles circulaires (direction des vents) et scalaires (vitesse du vent). Les auteurs effectuent une des interpolations directement sur les valeurs angulaires et apparemment ça marche, car par chance, toutes les valeurs qu'ils traitent se situent entre 0 et 180° (le fichier shapefile original peut être téléchargé).

Détail de la grille résultante

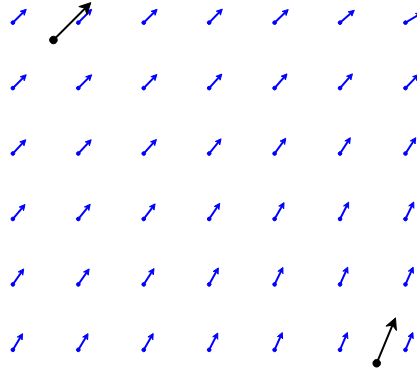
Mais si j'introduis quelques valeurs supérieures à 180° (puisque ce sont des vecteurs, en orange sur la figure), c'est une tout autre histoire:

Les flèches bleues sont le résultat de l'interpolation effectuée directement sur les valeurs angulaires et  donnent l'impression de « s'affoler ». Les flèches rouges sont le résultat du traitement effectué avec les méthodes exposées ci-dessus pour les données circulaires et le résultat se passe de commentaires. J'ai aussi utilisé un tel type de traitement dans  Trajectoires_de_schistosité (IPython Notebook)  et ça marche, puisque j'ai pris soin de limiter l'intervalle des données axiales.

Dans tous les autres cas, ma démarche est la suivante, basée sur la méthodologie élaborée pour l'interpolation de données circulaires par Gumiaux, C., Gapais, D., & Brun, J. P. (2003) dans Geostatistics applied to best-fit interpolation of orientation data., Tectonophysics, 376(3), 241-259).

Données de départ (axiales, des orientations):

Procédure:

1. La valeur de tous les angles est doublée;
2. Les valeurs des 2 cosinus directeurs sont calculées pour toutes les valeurs angulaires;
3. Les interpolations se font séparément sur ces valeurs (diverses méthodes d'interpolation spatiale possibles);
4. Les valeurs d'arc tangentes sont calculées pour chaque point de la grille en combinant les résultats des 2 interpolations obtenues;
5. Les valeurs résultantes sont divisées par 2.

Résultat

Problèmes rencontrés

Le principal problème réside dans le choix de la taille de la maille de la grille d'interpolation. Si elle est trop grande, on ne verra rien, si elle est trop petite, une fausse précision sera obtenue. Il est aussi nécessaire de s'interroger sur le sens à donner à cette interpolation: les valeurs sont-elles liées entre elles par quelque chose, se rapportent-elles à un même phénomène analysé, cette taille de maille est-elle significative pour ce phénomène, etc., bref, l'interpolation a-t-elle un sens réel et scientifique  ?

Pour aller plus loin

Il serait possible de calculer des trajectoires, comme exposé dans Geostatistics applied to best-fit interpolation of orientation data, mais cela dépasse le cadre de cet article.

fig 5 b) de Geostatistics applied to best-fit interpolation of orientation data

Conclusions

J'espère que ces quelques éléments vous donneront des clés pour aller plus loin dans ce domaine, immense et complexe de prime abord, car non limité à la géomatique.

Je fournis dans la suite quelques autres ouvrages ou tutoriels qui traitent de ce thème, pas toujours dans le domaine géomatique. Il suffit de chercher sur Internet « Circular Statistics ».

Signalons aussi qu'il y a des logiciels spécialisés comme Oriana (payant).

Site officiel : Statistics and Data Analysis in Geology, 3rd Edition, Davis, J.C. (2002), 5. Analysis of Directional Data
Site officiel : Statistical Analysis of Geographic Information with ArcView GIS and ArcGIS> (2005), Wong, D. W. S. Lee, J. , 7.3 Directional Statistics.
Site officiel : Statistics of Earth Science Data: Their Distribution in Time, Space and Orientation> (2013), Borradaile, G.J., 9 - Circular Orientation Data
Autres Liens : Lec 16 - Directional Statistics (pdf)
Autres Liens : Analysis of Directional Data (pdf, géologie)
Autres Liens : A MATLAB Toolbox for Circular Statistics (pdf)

licence Creative Commons Paternité-Pas d'Utilisation Commerciale-Pas de Modification 2.0 France