Répondre au commentaire

	Niveau	Intermédiaire
	Logiciels utilisés	Python Networkx nx_spatial
	Plateforme	Windows | Mac | Linux | FreeBSD

Comment transformer un shapefile, format sans topologie, en un réseau topologique (topologie de réseau,  voir la topologie dans « GRASS GIS : géométries, topologies et conséquences pratiques (vecteurs, rasters, volumes) ») de noeuds et d'arcs ou d'arêtes, c'est à dire un graphe mathématique ?

C'est la question que s'est posée Ben Reilly sur son blog pragmaticgeographer.posterous.com/geometric-network-geoprocessing suite à la question suivante posée sur un Forum et au manque d'outils fournis par ESRI  :

" I currently have a geometric network that I've been working with using the Utility Network Analyst tools. However, I've been trying to perform a few tasks that I've noticed the Network Analyst tools provide, but the Utility Network Analyst does not. Specifically, I want to place barriers at all locations specified by a point feature class - a functionality provided by the "Add Locations" tool in the Network Analyst Toolset. Is there a way to use the network analyst tools on a geometric network? "

Sa réponse a été :

"The answer, sadly, is no. As far as I can tell, ESRI has not released any geoprocessing tools for their Geometric Network".

Il a donc développé des modules Python pour le faire, utilitynetwork puis nx_spatial, basés sur la théorie des graphes.

Principes 

Nous ne nous occuperons pas ici d'exposer la théorie des graphes et ses  applications dans le domaine des SIGs , ce n'est pas le but du sujet.

Python, depuis le texte fondateur de Guido Van Rossum, le créateur du langage, « Python Patterns - Implementing Graphs », possède une riche bibliothèque pour traiter les graphes : wiki.python.org/moin/PythonGraphApi. Parmi ces modules, figure Networkx, un des plus complets et qui a été choisi par Ben Reilly pour créer ses modules. Il s'est aussi basé sur le module ogr pour l'importation des shapefiles et le module arcgisscripting pour les features class.

Avec les fichiers shapefile

Soit le shapefile de lignes suivant, figuré avec matplotlib (déjà vu sur le portail) :

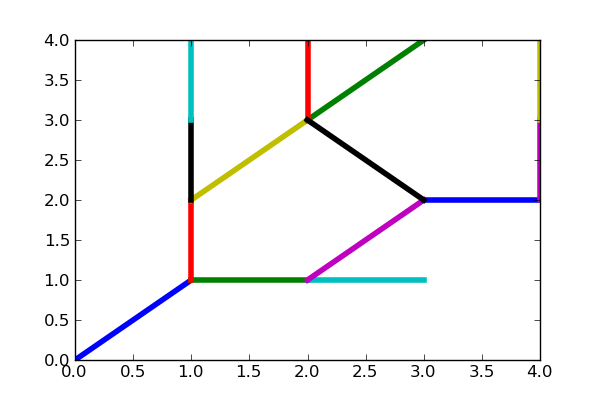
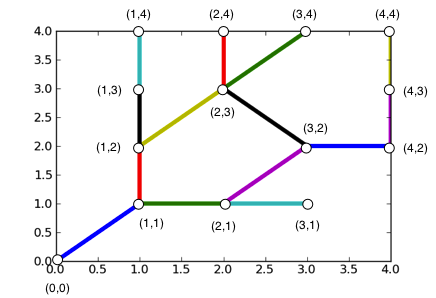
shapefile de lignes                                                  noeuds du shapefile

import nx_spatial as ns
 
#ouverture du fichier shapefile et création d'un graphe avec des noeuds et des arcs
G = nx.read_shp('meslignes.shp')
 
# noeuds du graphe résultant
print(G.nodes())
(1.0, 2.0), (3.0, 2.0), (0.0, 0.0), (3.0, 1.0), (4.0, 4.0), (2.0, 1.0), (2.0, 4.0),
(1.0, 3.0), (2.0, 3.0), (1.0, 4.0), (4.0, 3.0), (4.0, 2.0), (3.0, 4.0), (1.0, 1.0)]
 
 
# arcs du graphe résultant
print(G.edges())
[((1.0, 2.0), (1.0, 1.0)), ((3.0, 2.0), (2.0, 1.0)), ((3.0, 1.0), (2.0, 1.0)), ((4.0, 4.0),
(3.0, 4.0)), ((2.0, 1.0), (1.0, 1.0)), ((2.0, 4.0), (2.0, 3.0)), ((1.0, 3.0), (1.0, 2.0)),
((2.0, 3.0), (1.0, 2.0)), ((1.0, 4.0), (1.0, 3.0)), ((4.0, 3.0), (4.0, 2.0)), ((4.0, 2.0),
 (3.0, 2.0)), ((3.0, 4.0), (2.0, 3.0)), ((1.0, 1.0), (0.0, 0.0))]

Le résultat est un graphe orienté dont les étiquettes des noeuds sont formées par les valeurs x et y des points. Le module Networkx permet de dessiner les graphes résultants de diverses manières (networkx.lanl.gov/reference/drawing.html), avec entre autres, matplotlib ou  Graphviz (merveilleux programmes en C avec le langage DOT, pour matérialiser le graphe).

strict digraph  {
"(4.0,3.0)" -> "(4.0,4.0)"
"(4.0,3.0)" -> "(4.0,2.0)"
"(4.0,2.0)" -> "(3.0,2.0)"
"(3.0,2.0)" -> "(2.0,3.0)" 
"(2.0,3.0)" -> "(1.0,2.0)"
"(1.0,2.0)" -> "(1.0,1.0)" 
"(1.0,1.0)" -> "(0.0,0.0)"
"(3.0,4.0)" -> "(2.0,3.0)" 
"(2.0,4.0)" -> "(2.0,3.0)" 
"(3.0,2.0)" -> "(2.0,1.0)"
"(3.0,1.0)" -> "(2.0,1.0)"
"(2.0,1.0)" -> "(1.0,1.0)"
"(1.0,4.0)" -> "(1.0,3.0)"
"(1.0,3.0)" -> "(1.0,2.0)"
}

graphe G résultant avec noeuds et arcs (un peu enjolivé avec DOT qui permet de pratiquement tout faire) :

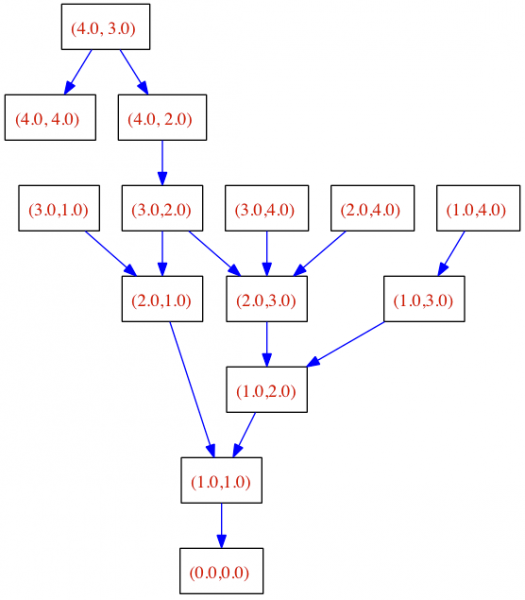
Ce graphe orienté peut ensuite facilement être transformé en graphe non orienté si tel est le souhait :

H = G.to_undirected()

graphe H résultant avec noeuds et arêtes (résultat brut du module) :

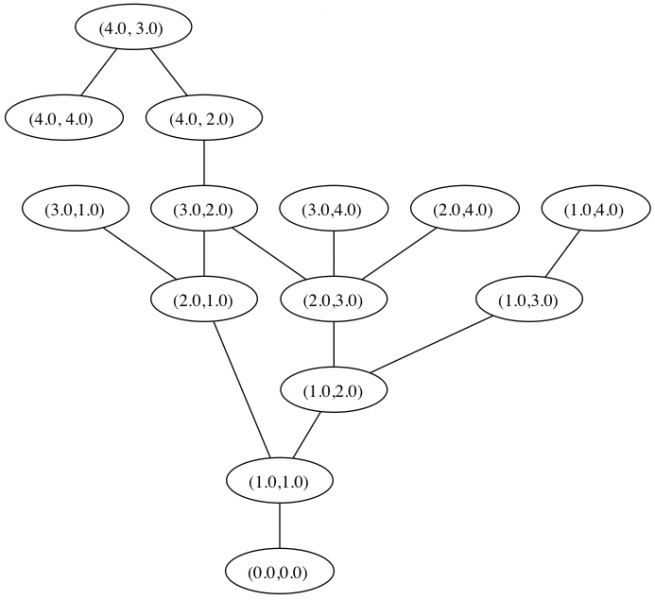
Notons que le module a été intégré à la version 1.4 de Networkx (networkx.lanl.gov/reference/readwrite.nx_shp.html)

import networkx as nx
G = nx.read_shp('meslignes.shp')
>>> print(G.nodes())
[(1.0, 2.0), (3.0, 2.0), (0.0, 0.0), (3.0, 1.0), (4.0, 4.0), (2.0, 1.0), (2.0, 4.0), (1.0, 3.0), (2.0, 3.0), (1.0, 4.0), (4.0, 3.0), (4.0, 2.0), (3.0, 4.0), (1.0, 1.0)]
>>> print(G.edges())
[((1.0, 2.0), (1.0, 1.0)), ((3.0, 2.0), (2.0, 1.0)), ((3.0, 1.0), (2.0, 1.0)), ((4.0, 4.0), (3.0, 4.0)), ((2.0, 1.0), (1.0, 1.0)), ((2.0, 4.0), (2.0, 3.0)), ((1.0, 3.0), (1.0, 2.0)), ((2.0, 3.0), (1.0, 2.0)), ((1.0, 4.0), (1.0, 3.0)), ((4.0, 3.0), (4.0, 2.0)), ((4.0, 2.0), (3.0, 2.0)), ((3.0, 4.0), (2.0, 3.0)), ((1.0, 1.0), (0.0, 0.0))]

Les deux modules sont légèrement différents car  l'original, nx_spatial, évolue plus vite.

Il y a aussi moyen de travailler avec les attributs d'un shapefile (networkx.lanl.gov/reference/functions.html#attributes et bitbucket.org/gallipoli/nx_spatial/src/b061ed50a851/nx_spatial/algorithms/attr_find.py).

Avec les features class d' ESRI

Ben Reilly montre aussi comment traiter de la même manière les features class d'ESRI, importées avec  le module arcgisscripting (gis.stackexchange.com/questions/210/alternatives-to-pgrouting) et bitbucket.org/gallipoli/nx_spatial/src/b5acb08beaa0/nx_spatial/readwrite/nx_esrifc.py ). N'étant pas sur Windows et ne disposant pas d'ArcGIS,  je ne peux que le citer.

Pour aller plus loin

Tous les algorithmes de Networkx peuvent en suite être utilisés sur ces graphes orientés et/ou non orientés (networkx.lanl.gov/reference/index.html). Notons en particulier tous ceux de parcours d'un graphe (networkx.lanl.gov/reference/algorithms.traversal.html ) et de plus court chemin (networkx.lanl.gov/reference/algorithms.shortest_paths.html, l'étiquette des noeuds permettant de calculer les distances euclidiennes).

Prenons l'exemple de la recherche du plus court chemin entre 2 noeuds en fonction de la distance.  Elle sera calculée avec l'algorithme de recherche A* (fr.wikipedia.org/wiki/Algorithme_A*). Les résultats sont évidemment triviaux dans notre exemple...

# les noeuds étant composés de 2 tuples Python ((x1,y1), (x2,y2)) la distance peut être 
# calculée avec la fonction :
def dist(a, b):
   (x1, y1) = a
   (x2, y2) = b
   return ((x1 - x2) ** 2 + (y1 - y2) ** 2) ** 0.5
 
print(nx.astar_path(G,(3.0,2.0),(1.0, 1.0),dist))
[(3.0, 2.0), (2.0, 1.0), (1.0, 1.0)]

Que se passe-t-il si l'on essaye de traiter 2 noeuds d'un graphe orienté non reliés par des arcs ?

print(nx.astar_path(G,(1.0,4.0),(4.0, 2.0),dist))
...
    raise nx.NetworkXNoPath("Node %s not reachable from %s"%(source,target))
networkx.exception.NetworkXNoPath: Node (1.0, 4.0) not reachable from (4.0, 2.0)
 
# il aurait été possible de le voir avec les diverses fonctions de Networkx comme :
nx.predecessor(G,(4.0,2.0))
{(1.0, 2.0): [(2.0, 3.0)], (3.0, 2.0): [(4.0, 2.0)], (0.0, 0.0): [(1.0, 1.0)], (2.0, 1.0): [(3.0, 2.0)], (2.0, 3.0): [(3.0, 2.0)], (4.0, 2.0): [], (1.0, 1.0): [(2.0, 1.0)]}
 
# ou 
nx.dfs_successors(G,(1.0,4.0))
{(1.0, 2.0): [(1.0, 1.0)], (1.0, 3.0): [(1.0, 2.0)], (1.0, 1.0): [(0.0, 0.0)], (1.0, 4.0): [(1.0, 3.0)]}

La solution est évidemment de transformer le graphe orienté en un graphe non orienté.

# recherche du plus court chemin
print(nx.astar_path(H,(1.0, 4.0),(4.0, 2.0),dist))
[(1.0, 4.0), (1.0, 3.0), (1.0, 2.0), (2.0, 3.0), (3.0, 2.0), (4.0, 2.0)]

Ces modules ne sont valables que pour des shapefiles de points (qui donneront des noeuds dont il est possible d'adjoindre des arcs ou des arêtes) et de lignes/polylignes (et donc pas de polygones).

Exportation

Avec les modules ogr ou shapely il est facile d'exporter les résultats en shapefiles (entre autres)

chemin =nx.astar_path(G,(3.0,2.0),(1.0, 1.0),dist)
# pour rappel [(3.0, 2.0), (2.0, 1.0), (1.0, 1.0)]
 
# avec shapely
from shapely.geometry import LineString
ligne = LineString(chemin)
print ligne.wkt
'LINESTRING (3.0000000000000000 2.0000000000000000, 2.0000000000000000 1.0000000000000000, 1.0000000000000000 1.0000000000000000)'
 
# avec ogr
from osgeo import ogr
ligne2 = osgeo.ogr.Geometry(ogr.wkbLineString)
 
from points in chemins:
   lignes2.AddPoint(points[0],points[1])
 
print ligne2.ExportToWkt()
'LINESTRING (3 2 0,2 1 0,1 1 0)'
 
etc...

Conclusions

Les réponses fournies aux questions sur gis.stackexchange.com/ montrent que cette solution peut constituer une alternative au PgRouting de PostGIS  (www.pgrouting.org/).

Tous les traitements ont été effectués sur Mac OS X avec Python 2.6.1, matplotlib, Networkx, shapely, ogr et Graphviz version 2.26.3 ( www.graphviz.org/Download_macos.php) et le visualisateur interactif  de Pixelglow, version 2.20.3  (www.pixelglow.com/graphviz/).

licence Creative Commons Paternité-Pas d'Utilisation Commerciale-Partage des Conditions Initiales à l'Identique Commerciale 2.0 France