Répondre au commentaire

GRASS GIS : introduction à l'algèbre des cartes (map algebra, r.mapcalc (et r3.mapcalc))

ven 22-04-2011 Martin Laloux

J'ai effeuré dans « GRASS GIS, géométries, topologies et conséquences pratiques (vecteurs, rasters, volumes)) », l'algèbre des cartes rasters (map algebra). Or, s'il y a un domaine qui semble très mal expliqué dans GRASS GIS, c'est celui-ci. Les seules références données datent de 1991 et 1992 (hormis « Neteler, M. & Mitasova, H. Open Source GIS A GRASS GIS Approach. Kluwer Academic Publishers, 2003») et l'on pourrait se dire, GRASS, quel ancêtre tout de même, passons à autre chose. Et pourtant, même si c'est clair qu'il manque de tutoriels, l'histoire montre qu'il suffit d'aller lire ceux des autres SIG pour comprendre et je vous conseille, cette fois, de lire les très belles explications du monde ESRI et autres. Une fois compris, il reste la nomenclature à appréhender. C'est cette introduction que je vais essayer d'aborder ici. Cette algèbre spatiale est en effet la base de tous les modules de traitement des rasters dans GRASS.

Avant de poursuivre et pour simplifier la vie des utilisateurs, il faut noter que les bienveillants concepteurs de GRASS ont généralement regroupé tous les traitements nécessaires à une tâche courante dans des nouveaux modules qui les effectuent de manière transparente (r.colors, r.resamp ou r.slope.aspect par exemple).

Un peu d'histoire, ou pourquoi personne n'a copié sur personne, mais, que tout le monde fait la même chose...

La théorie la plus complète de l'algèbre des cartes a été introduite en 1983 par Dana Tomlin (« A map algebra. In Proceedings of the 1983 Harvard Computer Graphics Conference, volume 2, pages 127–150, Cambridge , Massachusetts ») puis étendue et formalisée dans un livre en 1990 (« Geographic information systems and cartographic modeling. Prentice Hall, Englewood Cliffs, New Jersey »).

Il a personnellement participé à son implémentation dans GRASS GIS à la fin des années 1980. Mais, comme il a mis ses travaux dans le domaine public, ils ont aussi été à la base du GRID module d'ArcInfo, puis de l'extension Spatial Analist d'ESRI ou de AutoCAD MAP (www.urisa.org/hall/tomlin). Comme GRASS GIS et ArcInfo sont tous deux nés quasi en même temps (1982), on peut dire que personne n'a copié, mais que tous se sont basés sur les mêmes principes. ESRI a continué en enjolivant les interfaces avec style alors que GRASS est longtemps resté à la ligne de commande (comme ArcInfo). Ce n'est plus le cas.

Principes théoriques

L'idée de base de Tomlin est que les rasters peuvent être soumis à des opérations de type algébrique dont les résultats seront aussi des rasters. Il a élaboré une représentation formalisée de toutes les combinaisons possibles des cartes qu'il appelle les « layers » (couches) et un langage standardisé. Les rasters sont traités comme des grilles de points (quadrillage matriciel, pixel et voxel, voir « GRASS GIS, géométries, topologies et conséquences pratiques (vecteurs, rasters, volumes)) ». Son algèbre décrit des opérations arithmétiques sur des cellules, des groupes de cellules, ou des classes d'objets dans l'ensemble des cellules. Les opérations sont discriminées par leur portée spatiale :

les fonctions de portée locale s'appliquent à une cellule ;
les fonctions de portée focale ou de voisinage s'appliquent à des cellules voisines (mais non nécessairement adjacentes) ;
les fonctions de portée zonale s'appliquent à un ensemble de cellules de même valeur ;
les fonctions de portée globale s'appliquent à toutes les cellules d'une couche ;
les fonctions de portée incrémentale permettent, par exemple, de calculer le plus court chemin entre deux cellules non jointives (« The incremental operations compute a new value for every location as a function of its lineal, areal, or surficial form on a specified layer. These operations may indicate each location’s length or shape as part of a lineal network; its surface area, frontage, or shape as part of an areal pattern; or its slope, aspect, drainage direction(s), or volume as part of a surficial form » (D. Tomlin. Map algebra: one perspective. Landscape and Urban Planning, Elsevier Science, 30:3–12, 1994).

Tous les calculs sont effectués cellule par cellule. La portée détermine uniquement le nombre de cellules pris en considération.

Pour la suite de la théorie, je vous invite, avec plaisir, à consulter toutes les très belles et savantes explications d'ESRI et autres sur le sujet, puisque tout le monde se base sur les mêmes principes. Elles sont meilleures que ce que je pourrais vous exposer ici (je ne suis pas géomaticien de formation, mais « sur le tas » ). Je ne m'intéresserai ici qu'à la manière de procéder.

En pratique

Dans GRASS ce sont les modules r.mapcalc et r3.mapcalc qui permettent d'appliquer cette algèbre en ligne de commande en 2D et en 3D. GRASS dispose aussi depuis longtemps d'une interface graphique, semblable au « Raster Calculator » d'ESRI et affichable par le menu :

« Raster/Raster Map Calculator » (r.mapcalculator et r3.mapcalculator) .

Son apparence a changé au cours du temps et sa dernière mouture est illustrée ici (GRASS GIS 6.4.1 RC2).

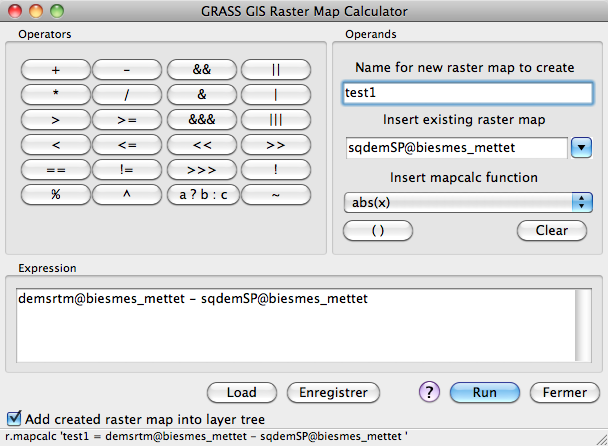
Cette interface graphique ne fait qu'envelopper la commande r.mapcalc comme on le voit dans le bas de la figure. Elle se présente toujours sous la forme :

(en ligne de commande, avec d'autres instructions combinées)

Dans l'exemple illustré :

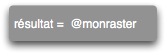
ou

signifie que le raster test1 (DEM dans le cas présent) sera le résultat de la soustraction des deux autres DEMs, cellule par cellule. Comme ce sont des rasters 2.5D, c'est la variable z qui sera considérée. Le fait de spécifier le jeu de données (MAPSET) (@biesmes_mettet) démontre qu'il y a moyen d'impliquer tous les rasters des jeux de données accessibles dans un secteur (LOCATION, voir « Les « geodatabases » de GRASS GIS, structure générale (LOCATION, MAPSET) et conséquences pratiques (changement de système de projection, etc.) ».

Variables

Quelles sont les variables qui peuvent être utilisés dans cette algèbre ?

des rasters comme dans le cas de demstrm@biesmes_mettet. Si le nom est univoque, il n' y a pas besoin de spécifier les noms des jeux de données (demstrm) ;
les catégories et les couleurs d'un raster. Dans l'exemple précédent, il s'agit du z, mais il aurait été tout aussi possible de travailler sur :
- les couleurs : dans GRASS, elles sont indépendantes du raster (placées dans un table, comme une autre variable) et modifiables à volonté ( opérateur #, tâche simplifiée avec r.colors, r.blend ou r.composite) ;
- les catégories : par exemple, si les attributs suivants sont associés à un raster :

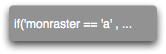
la commande

donnera les résultats 'a','b','c','d' d'où la possibilité de faire :

des constantes comme a = 123 ou des variables temporaires définies en cours du traitement ;
la notion géométrique de la région qui permet la création de fenêtres mobiles de travail avec les variables internes suivantes :

x(), y () : coordonnées x et y de la fenêtre de traitement;
col(), row() : colonnes et lignes de la fenêtre de traitement;
nsres() ewres() : résolution
la notion topologique de voisinage d'une cellule qui permet aussi la création de fenêtres mobiles de travail.

Il est très important de distinguer null() qui signifie littéralement rien de la valeur 0 qui est une valeur comme les autres.

Opérateurs et fonctions

Les opérateurs et les fonctions disponibles sont les suivants :

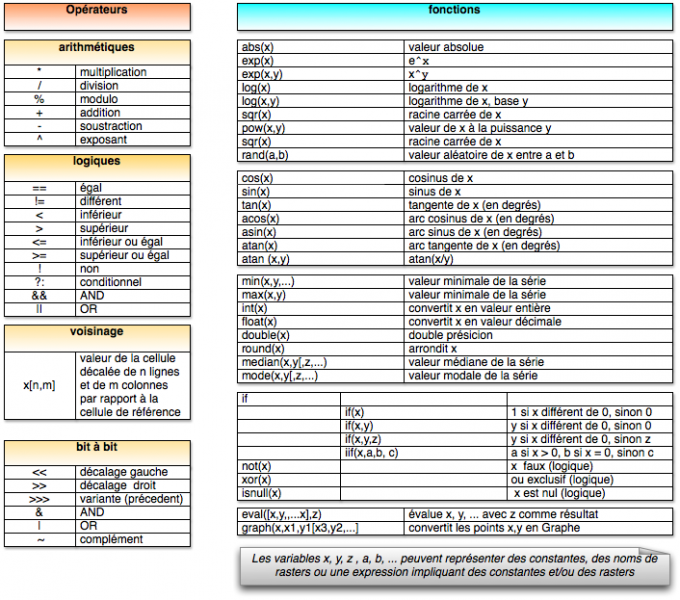
Dans la suite, nous allons examiner, de manière schématique, les divers traitements possibles.

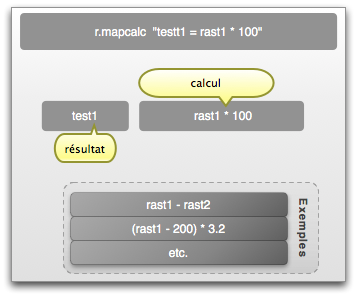
Calculs simples

Ils utilisent généralement les opérateurs arithmétiques ou binaires. Ils ne sont simples que vis-à-vis des autres opérations, car ils permettent de faire, par exemple, une analyse en composantes principales.

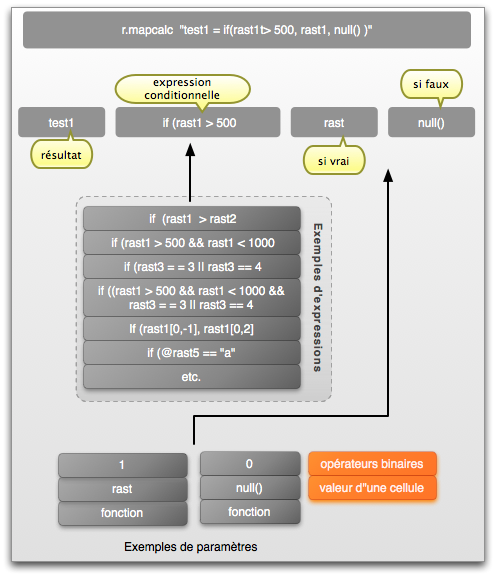
Expressions conditionnelles

Elles sont très importantes si l'on veut extraire des portions d'un raster ou le reclasser, à titre d' exemple. Un MASK est, en pratique, créé par une expression r.mapcalc.

Opérations de voisinage

C'est sans doute la notion la plus difficile à appréhender. Elle s'adresse au voisinage d'une cellule et propose donc des fonctions de voisinage.

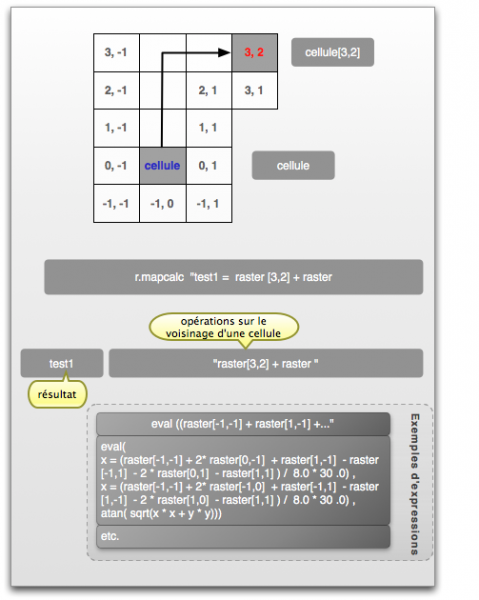
raster[3,2] signifie que l'on déplace le pointeur de 3 lignes vers le haut et de 2 colonnes vers la droite. Donc si je veux ajouter à chaque cellule du raster la valeur de la cellule qui se trouve dans la position relative [3, 2], la formule illustrée dans la figure sera utilisée ;
si l'expression devient plus complexe, avec plusieurs arguments et des variables temporaires pour capturer les résultats intermédiaires (x, y sur la fig.), eval() sera utilisé ;
cette démarche permet de se déplacer sur un raster et de faire des traitements sur ou à partir des cellules voisines de manière itérative (ce qui constitue une zone de traitement mobile) ;
elle est utilisée dans divers algorithmes :
- création de cartes de pentes et d'aspect (2e exemple de la fig.) à partir des élévations d'un MNT (calculs repris dans le module v.slope.aspect) ;
- création des cartes de flux (hydrologie, etc.) ;
- création de filtres spatiaux ;
- tout ce qui concerne la théorie des Graphes (plus court chemin, etc.) ;
- etc.

A titre d'exemple, voici les calculs utilisés par jamiepopkin.blogspot.com/2011/01/calculating-togographic-exposure-with.html pour calculer un élément d'une carte d'exposition topographique au vent (TOPEX) à partir d'un MNT d'une résolution de 25 x 25 mètres (ici dans une seule direction, N) :

r.mapcalc topex_n = "max(atan(((dem - dem[4,0])) / ((25 * 4))), atan(((dem[8,0] - dem)) / ((25 * 8))), atan(((dem[12,0] - dem)) / ((25 * 12))), atan(((dem[16,0] - dem)) / ((25 * 16))), atan(((dem[20,0] - dem)) / ((25 * 20))), atan(((dem[24,0] - dem)) / ((25 * 24))), atan(((dem[28,0] - dem)) / ((25 * 28))), atan(((dem[32,0] - dem)) / ((25 * 32))), atan(((dem[36,0] - dem)) / ((25 * 36))), atan(((dem[40,0] - dem)) / ((25 * 40))), atan(((dem[44,0] - dem)) / ((25 * 44))), atan(((dem[48,0] - dem)) / ((25 * 48))), atan(((dem[52,0] - dem)) / ((25 * 52))), atan(((dem[56,0] - dem)) / ((25 * 56))), atan(((dem[60,0] - dem)) / ((25 * 60))), atan(((dem[64,0] - dem)) / ((25 * 64))), atan(((dem[68,0] - dem)) / ((25 * 68))), atan(((dem[72,0] - dem)) / ((25 * 72))), atan(((dem[76,0] - dem)) / ((25 * 76))), atan(((dem[80,0] - dem) / ((25 * 80))))"

Les scripts et les boucles

Si l'on veut utiliser les boucles FOR ou WHILE dans les expressions, il est nécessaire de passer par un langage comme Sh, Bash, Python ou R. qui permettent, en plus, de combiner les opérations. Voici par exemple le traitement de oikos.inf.um.es/ pour créer des aires d'influence qui ne se recouvrent pas à partir d'une série de points :

for i in $(seq 60)
do
     r.mapcalc 'pto'$i'=if(mapa_ptos=='$i','$i',null())'
     r.buffer in='pto'$i out='S'$i'100' dist=100 --o
     r.mapcalc 'pto'$i'_100m=if(pto'$i'100!=0,'$i',null())'
     r.buffer in='pto'$i out='S'$i'1000' dist=1000 --o
     r.mapcalc 'pto'$i'_1000m=if(S'$i'1000!=0 ,'$i',null())'
     g.remove rast='pto'$i
     g.remove rast='pto'$i'100'
     g.remove rast='pto'$i'1000'
done

(voir aussi « Grass Gis, ses amis Python et R, ou la puissance d'un shell pas si "ringard" que ça... (traitement des données, géostatistiques and Co. » ou « Using R and r.mapcalc (GRASS) to Estimate Mean Topographic Curvature » casoilresource.lawr.ucdavis.edu/drupal/node/937)

Conclusions

J'espère que cette petite introduction vous aura permis de comprendre qu'une fois maîtrisée, cette algèbre permet de pratiquement tout faire (surtout si on y ajoute Python ou R). Le problème est le « une fois maîtrisée » car il faut encore une fois beaucoup fouiller pour trouver quelque chose de complet (ou assembler les petits morceaux trouvés de-ci de-là).

Les traitements sont moins faciles qu'avec les beaux habits des autres SIGs mais ils m'ont permis de comprendre et de maîtriser exactement ce que je fais ou ce que je veux faire (ce qui n'aurait pas été le cas avec les beaux habits). Ils sont gratuits, sans extension supplémentaire, et si l'on est habile en programmation, il est possible de participer au développement. Beaucoup de modules de GRASS GIS sont, en fait, des scripts combinant plusieurs traitement comme celui illustré précédemment, de même que ceux présentés sur grass.osgeo.org/wiki/GRASS_AddOns. Il est souvent intéressant de les analyser pour mieux comprendre.

L'algèbre spatiale 3D avec r3.mapcalc obéit aux mêmes principes.

Tous les traitements ont été effectués sur Mac OS X avec GRASS GIS 6.4.1 RC2 et Inkscape pour les figures.